Содержание курса

Глава 2. Механизмы радиоизлучения в астрофизических условиях

2.1. Распространение радиоволн в плазме. Генерация радиоизлучения плазменными колебаниями

2.2. Поляризация излучения

2.3. Тормозное излучение ионизованного газа

2.4. Циклотронное излучение

2.5. Синхротронное излучение

2.6. Излучение кривизны

2.7. Излучение в спектральных линиях атомов и молекул

2.8. Молекулярное мазерное излучение

2.9. Рассеяние излучения

В этой главе и всех последующих используется система единиц CGS.

2.1. Распространение радиоволн в плазме. Генерация радиоизлучения плазменными колебаниями

Пусть на облако полностью ионизованного газа (плазмы) падает плоская монохроматическая волна, распространяющаяся вдоль оси z. Электрическое поле волны Под действием этого поля электроны приходят в движение. Классическое уравнение движения электрона:

(2.1)

m – масса электрона, n_ст – частота столкновений в плазме (второе слагаемое в левой части уравнения описывает трение электрона об окружающую плазму, приводящее к затуханию колебаний).

Напомним также уравнения Максвелла:

;

(2.2)

В дальнейшем для простоты стрелки над векторами опускаем.

При решении уравнений Максвелла для случая распространения волны в проводящей среде (плазме) оказывается удобным ввести комплексную диэлектрическую проницаемость среды в виде:

(2.3)

Комплексная диэлектрическая проницаемость (2.3) равна квадрату комплексного показателя преломления, который, в свою очередь, состоит из обычного показателя преломления n (действительная часть) и коэффициента поглощения k (мнимая часть).

Вначале рассмотрим случай без магнитного поля (). Из решения уравнения движения для электрона (2.1) можно найти:

. (2.4)

Выражение для частоты столкновений n_ст определяется решением задачи о рассеянии:

(2.5)

где – средняя скорость электронов, а N — их концентрация. В условиях солнечной короны (N ~ 10⁸ см^–3) n_ст ~ 1/15 с^–1 << w для всего диапазона радиоволн, поэтому w² + n_ст² @ w².

Для волны, распространяющейся вдоль оси z в плазме с диэлектрической проницаемостью e¢ (2.3), решение уравнений Максвелла дает:

(2.6)

Выбираем верхние знаки в экспоненте из соображений исчезновения волны на бесконечности. Первое слагаемое в показателе экспоненты характеризует распространение волны в среде с показателем преломления

(2.7)

Величина

(2.8)

называется плазменной (ленгмюровской) частотой и характеризует частоту собственных колебаний плазмы. Плазменная частота зависит (помимо атомных констант) только от местной электронной концентрации. Приближенно

(2.9)

Таким образом, при w ³ w_p коэффициент преломления плазмы всегда заключен в пределах 0 £ n £ 1; при w < w_p коэффициент преломления становится мнимым. Это означает, что в амплитуде волны появится еще один экспоненциально затухающий множитель, и волна будет поглощена на расстоянии ~l. Волны с w < w_p в плазме распространяться не могут.

Величина в показателе экспоненты в (2.6) характеризует уменьшение амплитуды волны за счет поглощения в плазме при свободно-свободных переходах. Чтобы перейти к более привычному коэффициенту поглощения для интенсивности, необходимо взять квадрат модуля комплексной амплитуды электрического поля, тогда коэффициент поглощения удваивается, и получим:

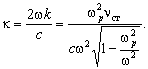(2.10)

Рассмотрим распространение электромагнитной волны в плазме с магнитным полем. В замагниченной плазме, кроме ленгмюровской частоты, возникает еще одна особая частота – гирочастота

(2.11)

Формула для приближенных оценок:

(2.12)

Используем приближение , что всегда выполняется в большинстве астрофизических объектов (в том числе в короне Солнца), но может нарушаться в активных областях на Солнце, где магнитные поля достигают сотен и тысяч Гаусс.

В плазме магнитное поле создает выделенное направление, и электрические свойства плазмы оказываются неодинаковыми вдоль и поперек поля. В этом смысле плазму можно уподобить кристаллу с двулучепреломлением, у которого показатели преломления различны для света, распространяющегося вдоль или поперек оптической оси. Так же, как в кристалле, произойдет разделение исходной волны на две волны (обыкновенную – 1 и необыкновенную – 2) с различными направлениями поляризации. Для каждой из волн будут иметь место разные показатели преломления.

Рассмотрим два случая: a = 0 и a = p/2 (a – угол между направлениями магнитного поля и распространения электромагнитной волны). Общий случай сложен, подробности можно найти в книге В.Л. Гинзбурга [16].

1) a = 0 (продольное распространение). Волна распадается на две поляризованные по кругу волны. Знаки "+" относятся к индексу 1 (обыкновенная волна), знаки "–" – к индексу 2 (необыкновенная волна).

. (2.13)

Для необыкновенной волны резко возрастает коэффициент поглощения вблизи w ~ w_H; поэтому на частотах вблизи гирочастоты первоначально неполяризованное излучение может приобрести круговую поляризацию. У необыкновенной волны направление круговой поляризации совпадает с направлением ларморовского вращения электронов вокруг магнитных силовых линий, поэтому волна испытывает повышенные потери энергии по сравнению с обыкновенной.

2) a = p/2 (поперечное распространение). Волна распадается на две волны с взаимно ортогональными линейными поляризациями. У обыкновенной волны вектор электрического поля – вектору магнитного поля, и магнитное поле не оказывает влияния на движения электронов. Поэтому для обыкновенной волны n₁ и k₁ совпадают с выражениями (2.13) для случая . Для необыкновенной волны:

; (2.14)

В случае поперечного распространения, из-за повышенного поглощения необыкновенной волны вблизи частоты может возникнуть линейная поляризация первоначально не поляризованного излучения.

2.2. Поляризация излучения

В предыдущем разделе мы встретились с понятием поляризации электромагнитного излучения. Рассмотрим подробнее поляризационные параметры и физические механизмы, влияющие на поляризацию излучения.

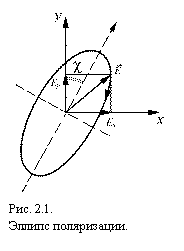В общем случае радиоизлучение может содержать две компоненты – неполяризованную и поляризованную. При распространении излучения конец мгновенного вектора электрического поля волны, измеренного в некоторой фиксированной точке пространства, описывает эллипс (рис. 2.1). Выберем систему координат, ось z которой направлена вдоль волнового вектора (то есть, совпадает с направлением распространения, перпендикулярным плоскости рис. 2.1), а оси x и y лежат в плоскости рисунка. Компоненты вектора в проекциях на оси x и y зависят от времени следующим образом:

(2.15)

Отношение E_0x/E_0y и разность фаз y_xy = y_x – y_y определяют позиционный угол эллипса c и отношение его осей p. Общая интенсивность I = I_пол + I_ест равна сумме поляризованной и естественной компонент; отношение r = I_пол/I называется степенью поляризации. В качестве величин, описывающих состояние поляризации, обычно принимают параметры Стокса I, Q, U, V:

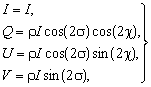(2.16)

где s =arctg p. Если антенна радиотелескопа принимает две ортогональные линейные поляризации вдоль осей x и y, то измеряемые интенсивности компонент равны

(2.17)

где черта означает усреднение по времени. Параметры Стокса:

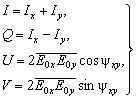(2.18)

Если антенна принимает два направления круговой поляризации – правую r (вектор в приближающейся волне вращается против часовой стрелки) и левую l (по часовой стрелке), то интенсивности право- и левополяризованной компонент равны, соответственно

(2.19)

а параметры Стокса выражаются через напряженности поля и , а также разность фаз y_rl право- и левополяризованных компонент:

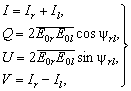(2.20).

В общем случае поляризованное излучение содержит смесь линейно и циркулярно поляризованных волн, то есть имеет эллиптическую поляризацию, состояние которой можно однозначно описать параметрами эллипса поляризации (рис. 2.1) либо параметрами Стокса.

Поляризованное излучение часто встречается в радиоастрономии. Как правило, источники синхротронного излучения (§2.5) имеют линейную поляризацию. Излучение активных областей на Солнце (§3.3) и космических гидроксильных мазеров (§5.5) бывает на 100% поляризовано по кругу.

Имеется ряд физических факторов, влияющих на состояние поляризации излучения. Так, суммарное синхротронное излучение источника с запутанным магнитным полем может обладать лишь небольшой степенью линейной поляризации, так как волны от разных частей источника, имеющие разные позиционные углы, складываясь, дают практически неполяризованное излучение.

Поляризация может меняться и во время распространения волны от источника к наблюдателю. Прохождение линейно поляризованного излучения сквозь среду, содержащую свободные электроны и магнитное поле, сопровождается фарадеевским вращением плоскости поляризации (из-за различия коэффициентов преломления n₁, n₂ и, для обыкновенной и необыкновенной волн, см. § 2.1). Угол поворота вектора поляризации на пути L волны частоты w определяется продольной компонентой H_║ магнитного поля (параллельной лучу зрения) и числом электронов на единичной площади в направлении наблюдателя:

(2.21)

Здесь H_║ выражается в микрогауссах; l — в парсеках; длина волны l — в метрах. Величина RM [рад/м²] – называется мерой вращения. Мера вращения очень велика в короне Солнца (где N ~ 10⁸–10¹⁰ см^–3, H ~ 1 Гс), там Dq достигает ~10⁶ радиан. В межзвездной среде для удаленных радиоисточников (пульсары) мера вращения порядка десятков и сотен радиан.

2.3. Тормозное излучение ионизованного газа

В ионизованном газе основной механизм поглощения и излучения в радиодиапазоне – свободно-свободные переходы (по-английски "free-free"). Излучение и поглощение происходит за счет изменения энергии свободных электронов, пролетающих вблизи ионов. Коэффициент поглощения равен

(2.22)

Здесь N_p — концентрация протонов, g_n – множитель Гаунта (он порядка единицы на сантиметровых волнах и достигает 10 на дециметровых волнах):

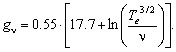(2.23)

Принимается, что распределение электронов по скоростям максвелловское с температурой T_e:

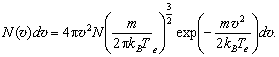(2.24)

Теперь учтем опущенное в (2.22) отрицательное поглощение, или индуцированное излучение. Скорости обоих этих процессов пропорциональны плотности излучения. По аналогии с дискретными переходами, свободно-свободный переход электрона можно рассматривать как переход между двумя уровнями (i и k), но не дискретными, а принадлежащие непрерывному спектру энергий. Запишем уравнение баланса, учитывая только радиационные процессы:

n_k A_ki + n_k B_ki r_ik = n_i B_ik r_ik. (2.25)

В левой части записано число переходов в единице объема за единицу времени вниз, с излучением квантов, в правой – переходы вверх, с поглощением. Здесь n_k, n_i – плотности атомов в состояниях k, i, r_ik –- плотность излучения на частоте перехода k®i. Перенесем второе слагаемое левой части в правую часть. Полное число фотонов, поглощаемых в спектральной линии, получается как разность поглощения и индуцированного излучения:

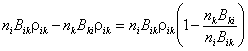(2.26)

Учтем известное соотношение между коэффициентами Эйнштейна:

(2.27)

g_i, g_k – статистические веса уровней. В случае термодинамического равновесия справедливо распределение Больцмана:

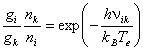
и правая часть формулы (2.26) при выполнении hn << k_BT_e (приближение Рэлея–Джинса) преобразуется в:

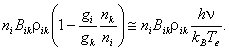(2.28)

Таким образом, вынужденные переходы k®i можно рассматривать как отрицательное поглощение, они приводят к уменьшению коэффициента поглощения и "просветлению" среды. В радиодиапазоне эффект отрицательного поглощения очень силен (особенно на низких частотах) и приводит к уменьшению коэффициента поглощения на несколько порядков величины. Все рассмотрение справедливо для двух любых значений энергии в континууме при максвелловском распределении электронов по скоростям. Итак, для учета отрицательного поглощения в радиодиапазоне необходимо домножить коэффициент поглощения (2.22) на . Подставив все значения констант, получим модифицированный коэффициент поглощения:

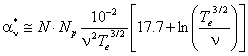(см^–1). (2.29)

Здесь N и N_p измеряются в см^–3, n — в Гц, T_e — в градусах Kельвина. Для чисто водородной плазмы N = N_p, и можно заменить произведение на N².

Можно сопоставить это выражение с полученной ранее классическим методом формулой (2.13) для коэффициента поглощения в плазме k (в случае, когда частота волны много выше плазменной частоты). В обеих формулах зависимость от частоты одна и та же.

При хаотическом движении электронов и ионов в плазме их траектории ориентированы под произвольными углами по отношению к наблюдателю. Поэтому результат сложения волн от элементарных актов взаимодействия "ион–электрон" дает в целом неполяризованное излучение.

Для расчета интенсивности излучения необходимо знать оптическую глубину объекта

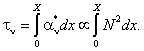(2.30)

Интеграл в (2.30) берется вдоль луча зрения в пределах излучающего облака. В конечном счете, оптическая глубина t_n по свободно-свободному поглощению определяется интегралом от квадрата электронной плотности, взятым вдоль луча зрения. Этот интеграл называется мерой эмиссии (ME – measure of emission). Единица измерения меры эмиссии см^–5; применительно к межзвездной среде чаще используют см^–6пк (см^-6 ´парсек).

Согласно (1.9), яркостная температура излучения равна

T_b = T_c [1 – exp(–t_n)]. (2.31)

В качестве температуры излучающего облака T_c берется величина электронной температуры T_e из максвелловского распределения электронов по скоростям (2.24). Коэффициент поглощения (2.29) сильно зависит от частоты (µ n^–2). На низких частотах, где велик, t_n >> 1, T_b @ T_c = const (для изотермического облака), интенсивность излучения определяется формулой Рэлея–Джинса (1.3) и пропорциональна n². На высоких частотах газ прозрачен, откуда T_b @ T_ct_n. В первом приближении t_n µ n^–2, и I_n не зависит от частоты. Правда, за 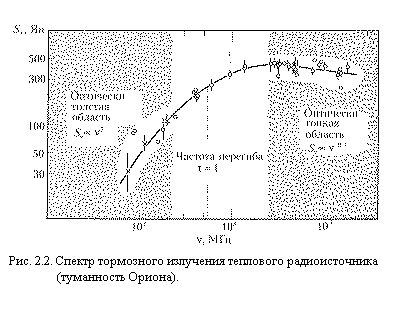счет множителя Гаунта имеет место логарифмическое падение интенсивности с ростом частоты. Иногда его аппроксимируют как I_n µ n^–0.1. Итак, спектр изотермического облака ионизованного газа, излучающего свободно-свободным механизмом, рэлей–джинсовский (µ n²) на низких частотах и плоский (слабо зависящий от частоты) на высоких частотах (рис. 2.2). Перегиб спектра происходит вблизи частоты, где t_n ~ 1. Частота перегиба связана простым соотношением с мерой эмиссии:

, (2.32)

n₀ в МГц, ME в см^–6пк. Если имеется возможность оценить размер излучающего облака вдоль луча зрения, то по известной частоте перегиба спектра источника n₀ можем оценить меру эмиссии ME и среднюю электронную плотность в источнике.

2.4. Циклотронное излучение

В магнитном поле электрон движется по винтовой траектории с осью на магнитной силовой линии. При этом он испытывает ускорение, что приводит к излучению. Механизм излучения заряженной частицы в магнитном поле называют в общем случае магнитотормозным Излучение нерелятивистской частицы (E << mc²), обычно называют циклотронным, для релятивистских частиц – синхротронным. Рассмотрим эти два предельных случая.

Частота дипольного излучения нерелятивистского электрона равна его ларморовской частоте вращения в магнитном поле с напряженностью H:

(2.33)

Для чисто кругового движения (когда скорость электрона вдоль поля равна нулю) радиус орбиты электрона

(2.34)

При v << c всегда Излучение можно рассматривать как излучение двух взаимно перпендикулярных гармонических осцилляторов, сдвинутых друг относительно друга по фазе на ½p, или как излучение электрического диполя с моментом , вращающегося вокруг силовой линии с частотой w_H. Средняя за период интенсивность циклотронного излучения

(2.35)

где a – угол между направлением магнитного поля и волновым вектором . Излучение происходит на частотах вблизи w_H. Более подробная теория [15, 18] показывает, что излучение также имеет место и на гармониках гирочастоты, то есть на частотах

w = sw_H,

где s = 2, 3,… Интенсивность излучения быстро спадает с увеличением номера гармоники s. Таким образом, спектр циклотронного излучения состоит из дискретных спектральных линий на гирочастоте и на ее гармониках.

Циклотронный мазер. При некоторых условиях в замагниченной плазме возможен эффект усиления магнитотормозного излучения. Примером этого является случай потоковой неустойчивости, когда заряженные частицы имеют распределение по скоростям вида

, (2.36)

где T_s, N_s и m – температура, концентрация и масса частиц в потоке. Распределение (2.36) отличается от максвелловского распределения наличием слагаемого в экспоненте. В случае параллельности коэффициент поглощения на частоте n будет

, (2.37)

а интенсивность излучения

. (2.38)

Если n_jb_scosa > 1, коэффициент поглощения становится отрицательным, а система поток–плазма начинает усиливать излучение. Частицы в потоке начинают излучать когерентно, то есть в фазе, и складываются амплитуды (а не интенсивности) волн, генерируемых отдельными частицами. Имеет место мазерный эффект.

Механизм мазерного усиления в замагниченной плазме применяется для объяснения высоких яркостных температур в ряде астрофизических объектов, где присутствует сильное магнитное поле и потоки частиц. Прежде всего, это солнечное радиоизлучение (шумовые бури I типа), спорадическое излучение Юпитера (T_b до 10¹⁵ K), радиоизлучение магнитосферы Земли на километровых волнах (T_b до 10¹⁷ K), пульсары, вспыхивающие звезды (типа UV Cet) и тесные двойные системы (типа RS CVn).

2.5. Синхротронное излучение

Синхротронный механизм – один из наиболее часто встречающихся в астрофизике. Он работает везде, где есть для этого условия: релятивистские электроны и магнитное поле. Основные астрофизические объекты, излучающие синхротронным механизмом: облака релятивистских электронов, выброшенные из активных областей на Солнце (всплески IV и V типов), магнитосферы планет-гигантов, галактический диск (на дециметровых и метровых волнах), остатки вспышек сверхновых, пульсары, нормальные галактики, радиогалактики, квазары.

Магнитотормозное излучение, рассмотренное в предыдущем параграфе, происходит на гирочастоте и ее гармониках и практически изотропно. Однако для релятивистских электронов ситуация качественно изменяется.

Вначале рассмотрим излучение одного электрона в случае, когда угол c между вектором скорости электрона и вектором магнитного поля равен 90°. Под действием силы Лоренца электрон вращается вокруг силовой линии магнитного поля. Вследствие релятивистского сокращения углов излучение электрона будет сосредоточено в узком конусе вокруг вектора мгновенной скорости электрона. Угол раствора конуса (в радианах)

, (2.39)

где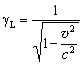 – фактор Лоренца, представляющий собой меру энергии релятивистского электрона (E = mc²g_L).

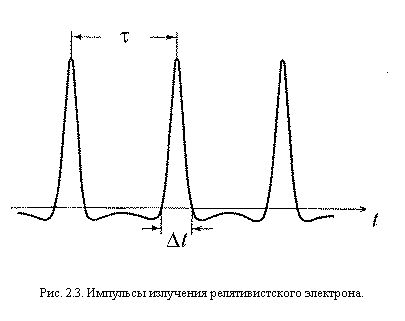
Наблюдатель на луче зрения, перпендикулярном к вектору , видит короткие импульсы с периодом , длительность каждого импульса (рис. 2.3). Множитель g_L учитывает релятивистское замедление течения времени.

В случае, когда электрон движется под произвольным (не очень малым) углом c ("питч-угол") к вектору , будет работать лишь компонента , перпендикулярная к вектору скорости : H_^ = Hsinc. Соответственно, период следования импульсов изменится вследствие эффекта Доплера за счет движения электрона вдоль силовых линий со скоростью v_|| = vcosc. Электрон как бы догоняет испущенный импульс (см. рис. 2.4):

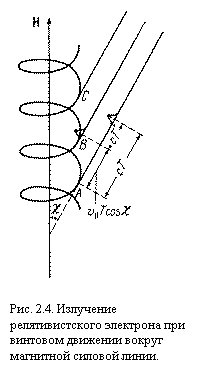
, (2.40)

так как v ~ c. Круговая частота следования импульсов

. (2.41)

Приведенное рассмотрение пригодно для углов c (выраженных в радианах) >> 1/g_L. Изменение периода следования импульсов скажется в первую очередь на спектре и должно быть учтено при усреднении по питч-углам.

Излучение, состоящее из коротких импульсов (рис 2.3), содержит множество частотных гармоник и обладает широким спектром с максимумом вблизи частоты . Для получения формы спектра единичного релятивистского электрона необходимо разложить последовательность импульсов в интеграл Фурье. При этом учитывается форма каждого импульса, определяемая, в свою очередь, вращающейся диаграммой направленности излучения электрона. Теория синхротронного излучения [15] дает следующее выражение для спектральной плотности мощности излучения:

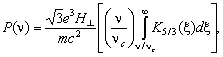(2.42)

где K_5/3 – функция Бесселя мнимого аргумента порядка 5/3, H_^ == Hsinc – составляющая магнитного поля, перпендикулярная к вектору скорости электрона (угол c не слишком мал),

. (2.43)

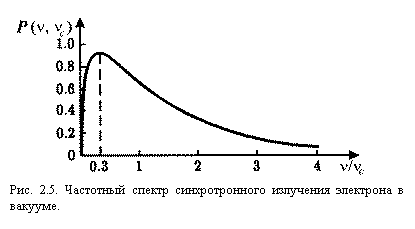
Характерная частота n_c не есть частота максимума спектра P(n), частота максимума . Функция P(n), выраженная в безразмерных единицах, представлена на рис. 2.5. Для релятивистских электронов, излучающих в межзвездной среде, типичные значения H ~ 10^–5–10^–6 Гс, g_L ~ 10³–10⁵.

Излучение электрона линейно поляризовано. Вектор поляризации расположен в картинной плоскости перпендикулярно направлению магнитного поля, так как изменение вектора электрического поля максимально именно в плоскости ларморовской орбиты электрона.

Степень поляризации .

Для перехода к ансамблю релятивистских электронов, имеющему некоторое распределение по энергиям N(E), необходимо провести усреднение функции P(n) по N(E). В функции P(n) зависимость от энергии входит через фактор Лоренца g_L, содержащийся в величине n_c. Интенсивность излучения ансамбля равна

, (2.44)

где L – размер излучающей области вдоль луча зрения. Предполагается, что источник прозрачен для собственного синхротронного излучения. Это условие всегда выполняется для диска Галактики, но может нарушаться в некоторых компактных внегалактических источниках.

В астрофизических условиях спектр релятивистских электронов обычно представляется степенной функцией:

N(E)dE = KE^–gdE. (2.45)

Такой вид спектра обусловлен особенностями механизмов ускорения частиц (§5.1). Для спектра излучения теория дает

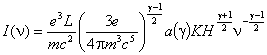. (2.46)

Следовательно, магнитотормозное излучение ансамбля релятивистских электронов со степенным распределением по энергиям вида (2.48) имеет степенной спектр I(n) µ n^–a, где величина называется спектральным индексом.

Полное выражение для функции a(g) можно найти в [15]. В широком интервале частот функция a(g)~0.1. Вид функции a(g) различен для однородного и хаотически ориентированного ("запутанного") поля. В частности, она учитывает распределение электронов по питч-углу, так как он входит в величину H_^.

В случае однородного магнитного поля излучение ансамбля электронов также поляризовано; степень поляризации равна

.

Диапазону 2 < g < 3 отвечает степень поляризации около 70%. В случае хаотически ориентированного поля поляризация отсутствует. На практике реализуется промежуточный случай.

У всех источников синхротронного излучения на низких частотах наступают отклонения от степенного спектра ("завал"). Низкочастотный завал может быть обусловлен тремя причинами:

1. Тормозное поглощение в ионизованном газе на частотах n < n_max спектр имеет вид .

2. Эффект Разина–Цытовича. Предыдущее рассмотрение проведено для частиц, излучающих в вакууме. Для частот ниже

. (2.47)

показатель преломления меньше единицы и фазовая скорость больше, чем с. Частица "отстает" от излучения, и при n < n_cr

. (2.48)

В межзвездной среде этот эффект несуществен.

3. Синхротронное самопоглощение. При n < n_cr .

2.6. Излучение кривизны

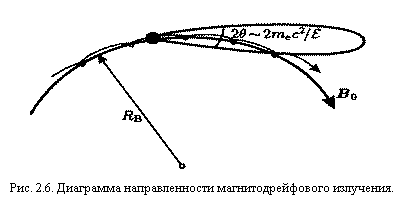
Излучение кривизны, называемое также магнитодрейфовым, аналогично синхротронному (рис. 2.6). При движении вдоль искривленной силовой линии с радиусом кривизны R_B электрон излучает, как если бы он вращался по орбите с радиусом R_B. Роль гирочастоты играет величина . Ниже критической частоты

,

спектр имеет степенную форму с показателем 1/3:

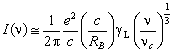, (2.49)

а при n > n_c спектр экспоненциальный:

(2.50)

Излучение кривизны имеет место в магнитосферах пульсаров, для которых характерны значения параметров n_c ~ 1 ГГц, g_L ~ 10³.

2.7. Излучение в спектральных линиях атомов и молекул

Коэффициент поглощения в линии k_n имеет резкую зависимость от частоты: вблизи центра линии n_ul он велик, а в крыльях — мал. При доплеровском профиле:

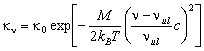(2.51)

Величина в расчете на один атом (молекулу) равна

. (2.52)

Здесь u и l – соответственно, верхний и нижний уровни перехода, A_ul – вероятность спонтанного перехода u→l, – средняя тепловая скорость атомов (молекул) массой M.

Интенсивность излучения зависит от температуры возбуждения перехода T_x. При термодинамическом равновесии отношение населенностей уровней равно

. (2.53)

В центре сильной линии яркостная температура излучения равна температуре возбуждения. Линия имеет плоскую вершину; по которой можно оценить T_x и затем температуру и плотность газа. В частотах крыльев линия может быть прозрачна. Если линия прозрачна на всех частотах, то по интегральной интенсивности профиля можно оценить количество излучающих атомов (молекул) на луче зрения в столбе сечением 1 см² – так называемую "столбцовую плотность" (column density). Подробнее этот вопрос мы рассмотрим ниже (§5.2) при обсуждении линии l = 21 см нейтрального водорода.

2.8. Молекулярное мазерное излучение

При сильном отклонении от термодинамического равновесия возможно нарушение больцмановского распределения по уровням. Может реализоваться случай инверсии населенностей, когда температура возбуждения T_x некоторого перехода становится отрицательной. Это соответствует избытку населенности ("инверсии населенностей") верхнего уровня u относительно нижнего уровня l по сравнению с формулой Больцмана. Степень инверсии населенностей характеризуется величиной

. (2.54)

Инверсия может создаваться при помощи некоторого механизма накачки (излучением или столкновениями с частицами окружающего газа). При прохождении фонового радиоизлучения на частоте перехода n_ul возникает лавина вынужденных переходов u→l, и излучение многократно усиливается. Имеет место мазерный эффект (maser – Microwave Amplification by Stimulated Emission of Radiation). Условия, благоприятные для накачки молекул OH, H₂O и некоторых других, существуют в областях звездообразования, вблизи молодых звездных объектов, а также в газопылевых оболочках звезд на поздней стадии эволюции – красных гигантов и сверхгигантов (§§ 5.5, 6.1).

Уравнения, описывающие перенос мазерного излучения в одномерном случае (в общем случае зависящие от времени):

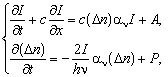(2.55)

член с A учитывает влияние спонтанных переходов (в мазере им обычно пренебрегают, так как основная роль принадлежит вынужденным переходам), P – мощность накачки (количество молекул, накачанных на верхний уровень u в 1 см³ за 1 с), I, Dn, P – функции x и t, a_n – коэффициент усиления мазера; второе уравнение отражает конкуренцию двух процессов: уменьшения Dn в результате вынужденных переходов сверху вниз и его увеличения за счет накачки. В стационарном случае производные по времени обращаются в ноль. Имеются два предельных решения:

а) ненасыщенный мазер (скорость накачки велика и превышает скорость вынужденных переходов):

(2.56)

– коэффициент мазерного усиления, A_ul – вероятность спонтанного перехода u®l, dn – ширина мазерной линии; нарастание интенсивности с расстоянием происходит экспоненциально;

б) насыщенный мазер (скорость вынужденных переходов превосходит частоту актов накачки, то есть практически вся мощность накачки используется для мазерного усиления):

, (2.57)

где S_p – скорость накачки (в расчете на одну молекулу за одну секунду), B – эйнштейновский коэффициент вынужденного перехода (2.39), W – телесный угол, в котором распространяется мазерное излучение; интенсивность растет линейно в зависимости от расстояния.

В космических источниках чаще реализуется случай насыщенного мазера: при значительном росте интенсивности условие случая (б) достигается очень быстро, и мазер переходит из ненасыщенного режима в насыщенный.

Для накачки мазера и создания инверсии населенностей некоторого перехода необходимы неравновесные условия (например, облучение анизотропным потоком радиации с непланковским спектром, различие температур газа и поля излучения и т.д.). Механизмы накачки делятся на радиативные (возбуждение излучением) и 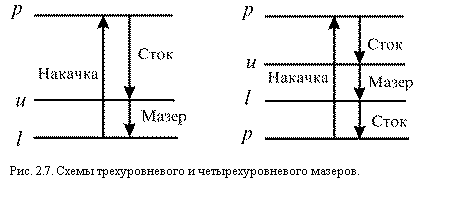столкновительные (возбуждение столкновениями с частицами окружающего газа). В цикле накачки, помимо "сигнальных" уровней перехода u®l, участвуют другие, обозначенные p на рис. 2.7. В случае, когда уровень l представляет собой основное состояние молекулы (пример – линии OH l = 18 см), мазер можно считать трехуровневым; в других случаях в накачке участвуют как вышележащие, так и нижележащие уровни. Реально p могут представлять собой целые группы уровней.

Известны источники мазерного радиоизлучения (в линиях молекул OH, H₂O, CH₃OH, SiO и H₂CO) в областях звездообразования, в окрестностях молодых звездных объектов, и в газопылевых оболочках звезд поздних спектральных классов – красных гигантов и сверхгигантов (в линиях OH, H₂O, SiO и HCN). Особенно сильные мазеры OH, H₂O и H₂CO ("мегамазеры") обнаружены в некоторых активных галактиках (§7.1).

2.9. Рассеяние излучения

Излучение в астрофизических условиях часто испытывает не только поглощение, но и рассеяние. Кратко рассмотрим два механизма рассеяния.

Томсоновское рассеяние. Этот вид рассеяния происходит на свободных электронах без изменения частоты. Сечение томсоновского рассеяния

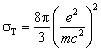= 6.65×10^–25 см² (2.58)

не зависит от частоты.

Эффект Комптона. В прямом эффекте Комптона при взаимодействии кванта с неподвижным электроном происходит уменьшение частоты кванта. Измененная частота кванта

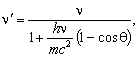(2.59)

q – угол рассеяния кванта. Эффект Комптона существенен только в тех случаях, когда велика оптическая толща по томсоновскому рассеянию, это имеет место, как правило, на достаточно высоких частотах – в ультрафиолетовом и рентгеновском диапазоне, а в радиодиапазоне эффект Комптона незначителен: на этих частотах работает лишь томсоновское рассеяние. Тем не менее, здесь эффект Комптона рассматривается, поскольку он важен в некоторых задачах, имеющих отношение к радиоастрономии, в частности, при рассмотрении механизмов ускорения релятивистских электронов, генерирующих синхротронное излучение.

Если электрон движется и его кинетическая энергия превышает энергию кванта, то возможен процесс передачи энергии от электрона к квантам поля излучения. Один из вариантов этого процесса – синхротронное излучение, другой – обратный эффект Комптона. Энергетические потери электрона на обратный эффект Комптона равны

. (2.60)

где u_rad – плотность энергии поля излучения в единицах mc², E – энергия электрона. Время жизни электрона из-за комптоновских потерь

. (2.61)

Отношение синхротронных потерь электрона к потерям на обратное комптоновское рассеяние

, (2.62)

где J – угол между вектором скорости электронов и направлением локального магнитного поля.

Обратный эффект Комптона может проявляться в ядрах галактик и квазаров в виде перекачки энергии от релятивистских частиц к квантам поля реликтового излучения с T_b = 2.7 K. В результате энергия квантов возрастает так, что радиокванты преобразуются в рентгеновские, а мощность синхротронного излучения электронов ограничивается величиной T_b ~ 10¹² K.

Принципиальное отличие эффектов рассеяния от эффекта свободно-свободного поглощения: томсоновское и комптоновское рассеяние происходит на свободных электронах, а свободно-свободное поглощение – при взаимодействии излучения со свободным электроном в поле иона, в этом процессе электрон и ион как бы образуют на время взаимодействия диполь.