| Вернуться к оглавлению |
| Перейти к следующей задаче |
|
Задача №06
ИССЛЕДОВАНИЕ ФОТОУМНОЖИТЕЛЯ
Введение
Фотоумножитель - это прибор, в котором падающее на него электромагнитное
излучение (оптического диапазона) преобразуется в многократно усиленные
импульсы тока. Регистрация этих импульсов может осуществляться либо путем
их усреднения по времени (метод постоянного тока), либо путем счета
отдельных фотонов (метод счета фотонов). И в том и в другом методе по
результатам измерений можно определить поток
излучения, падающего на катод ФЭУ, который считается
пропорциональным в первом случае
- силе тока через ФЭУ, во втором - числу импульсов, рождающихся
за единицу времени.
Рассмотрим конструкцию фотоумножителя типа ФЭУ-79, который часто
используется в астрономической практике (рис.1).
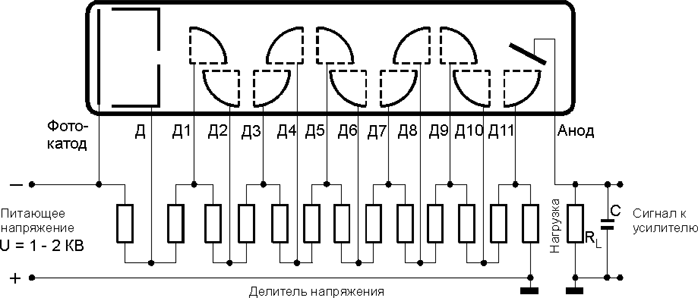
Рисунок 1: Конструкция фотоумножителя типа ФЭУ-79
Свет попадает на фотокатод ФЭУ, находящейся в стеклянной
вакуумной камере. Электроны, выбиваемые с
катода, ускоряются электическим полем, двигаясь от одного динода
к другому и выбивая из них новые электроны. В итоге один фотон,
отдавший энергию одному выбитому электрону, рождает целый каскад
электронов на выходе, воспринимаемый как очень короткий электрический
импульс.
Количество каскадов усиления у ФЭУ-79 (т.е. количество динодов) равно 11.
Фотокатод - полупрозрачный мультищелочной. Фотокатод характеризуется
квантовым выходом e, равным среднему отношению числа
фотоэлектронов n,
выбиваемых в результате фотоэффекта к числу упавших фотонов:
e = nфэ/nфот .
Характерный квантовый выход отечественных ФЭУ Ј 10%.
Основной принцип работы фотокатода - внешний фотоэффект. Однако в
нормальных рабочих температурах (0-20° С) бывает
существенен и другой процесс, вызывающий появление в катодной
камере электронов - это термоэмиссия фотоэлектронов с фотокатода.
Этот эффект создает темновой ток ФЭУ, т.е. ток на выходе при
отсутствии излучения на входе. Кроме этого, вклад в темновой ток
дает термоэмиссия с динодов, а при высоких напряжениях могут
стать существенными также различные разрядные процессы в колбе
ФЭУ. Для уменьшения темнового тока существуют два принципиальных
метода:
В конструкции ФЭУ-79 применен второй метод, что не исключает, естественно,
и возможности использования первого. Катодная камера ФЭУ-79 является
электронно-оптической линзой, которая "строит" на первом диноде
изображение не всего катода (диаметром 30 мм), а только небольшой его
центральной части (диаметром около 6 мм). Это ограничивает рабочую область
фотокатода. Чувствительность самого фотокатода по площади можно считать
постоянной, но из-за применения метода б) она становится неравномерной и
определяется зонной характеристикой. Положение области максимальной
чувствительности зависит от положения оси электронной линзы. Для каждого
данного ФЭУ оно определяется отдельно.
Коэффициент вторичной эмиссии, т.е. коэффициент усиления одного каскада
ФЭУ, невелик (3-5), однако большое число динодов позволяет достигать общего
усиления от 106 до 108 раз. Коэффициент вторичной эмиссии зависит от энергии
первичных электронов, т.е. от ускоряющего междинодного напряжения.
Поэтому коэффициент усиления всего ФЭУ зависит от напряжения питания
Uпит. Потенциалы динодов задаются делителем напряжения.
Характерные напряжения питания ФЭУ - от 1 до 2-3 кВ.
В астрономии ФЭУ получили широкое распространение в качестве
приемников излучения широкого диапазона спектра (от ближнего
ультрафиолета до ближней ИК области).
В настоящее время практически всегда используется метод счета фотонов,
который имеет следующие основные достоинства перед методом
регистрации тока:
Поэтому в дальнейшем мы будем рассматривать основные характеристики
ФЭУ, работающего в режиме счета фотонов.
Зависимость выходного сигнала (скорости счета n имп./с) от напряжения питания
Uпит называется счетной характеристикой фотоумножителя (рис.2)
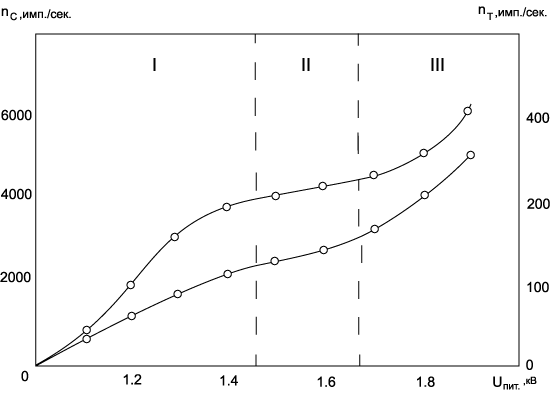
Рисунок 2: Счетная характеристика фотоумножителя
Для объяснения формы счетной характеристики рассмотрим другую
важную характеристику ФЭУ - амплитудное распределение выходных
импульсов n(A) , где n - число импульсов на выходе ФЭУ с
амплитудой от A до A+dA. На рис.3 приведены типичные
зависимости n(A) для сигнальных и темновых импульсов (кривые 1
и 2 соответственно). Видно, что зависимости имеют две выделенные
точки A1, A2 . Поведение функции от 0 до A1
определяется импульсами, которые возникают в результате
термоэмиссии электронов с динодов. Эти импульсы имеют малую
амплитуду, так как усиливаются не на всех каскадах ФЭУ. Для А > А1 зависимость nt(A) определяется в основном импульсами,
которые возникают в результате усиления катодных термоэлектронов.
В этом случае nt(A) имеет вид распределения Пуассона со
средней амплитудой A2 . Становится понятным, каким образом
можно избавиться от динодных импульсов: установить на выходе ФЭУ
пороговую схему (дискриминатор), которая не пропустит импульсы с
амплитудой A < Ad=A1 . Современная электронная техника позволяет
создавать такие дискриминаторы. Амплитудное распределение для
сигнальных импульсов катодного происхождения, которые несут
информацию об измеряемом источнике, сдвинуто в область больших
амплитуд. Видно, что дискриминация импульсов с амплитудой A < A1
не уменьшает существенно число сигнальных импульсов.
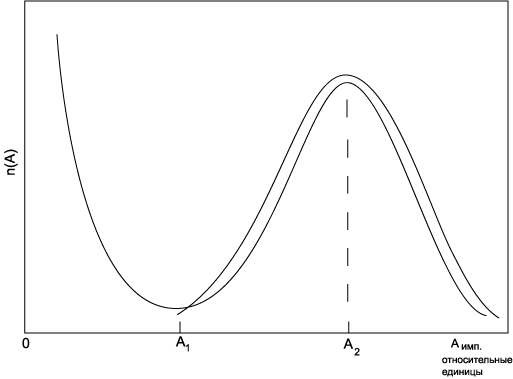
Рисунок 3: Зависимости n(A) для сигнальных и темновых импульсов (кривые 1
и 2 соответственно)
Амплитудное распределение импульсов n(A) является
дифференциальной характеристикой, т.е. n(A)dA=N(A+dA)-N(A) или n(A)=dN/dA, где N(A) - число импульсов с
амплитудой, меньшей чем А. Если измерить на выходе ФЭУ число
импульсов, прошедших пороговую схему с уровнем дискриминации
Ad , то, изменяя Aд, можно получить
N(Ad) ~ тAdҐ n(A)dA , весьма похожее по форме
на зеркальное отражение счетной характеристики. При этом точка
A1 будет соответствовать минимуму производной dN/dA ,
а точка A2 - максимуму.
Сходство счетных характеристик и интегральных амплитудных распределений
выходных импульсов ФЭУ не случайно. Счетная характеристика снимается при
постоянном уровне дискриминации Aд = const, но при изменяющемся напряжении
питания, а амплитудные распределения - наоборот: при Uпит=const, но при
изменяющемся Aд. Амплитуды импульсов на выходе ФЭУ определяются
средним коэффициентом усиления Kу ФЭУ. В первом приближении
измеряемые
амплитуды пропорциональны Kу), который увеличивается с ростом Uпит,
поэтому при счете импульсов увеличение Uпит эквивалентно уменьшению Aд.
Следовательно, счетную характеристику можно считать аналогом амплитудного
распределения. Становится понятным и существование трех основных зон на
счетной характеристике (рис.2): 1-й зоны (считаются катодные импульсы большой амплитуды), 2-й зоны
(считаются практически все катодные (сигнальные и темновые) импульсы), 3-й
зоны (начинается счет динодных и темновых импульсов).
Для идеального ФЭУ значение nс(U) в области 3 должно стремиться к некоторому
пределу (подсчитываются все импульсы). Однако для реальных ФЭУ этого не
происходит, так как при больших Uпит внутри колбы возникают разрядные
процессы, вызывающие появление на выходе импульсов большой амплитуды
( Aраз > A2 ).
Увеличение числа импульсов объясняет загиб вверх счетной
характеристики nc(U) в области 3 (рис.2). Это зона неустойчивой
работы ФЭУ, и ее стараются избегать.
По счетным характеристикам выбирается рабочее напряжение питания
ФЭУ Uр. На кривых nс(U) и nт(U) находят точки U0
и U1, в которых dnc/dU и dnt/dU минимальны. Величина
U1 будет соответствовать такому напряжению, при котором A1 » Aд (рис.3) Обычно U0 і U1 . Если расхождение между
ними не превышает 150-200 В, то выбирается рабочее напряжение
Uр = U0 » U1, ( ~ 1500 В), соответствующее такому
режиму работы ФЭУ, когда через дискриминатор проходят практически
все импульсы катодного происхождения (как сигнальные, так и
темновые), влияние разрядных процессов минимально, и выходной
сигнал наименее чувствителен к флуктуациям питающего напряжения
(так как dn/dU минимальна).
Если U0 > U1 и при напряжении U1 счетная характеристика nc(U)
"вышла" на некоторый
приблизительно постоянный уровень, то напряжение питания обычно
выбирается равным U1, так как при этом еще не начался счет темновых импульсов
динодного происхождения. Но если значение измеряемого сигнала nс >> nт, то
допустимо установление рабочего напряжения Uр=U0 (это соответствует измерению
излучения от ярких источников).
Кроме ФЭУ, в состав счетчика фотонов входят также:
На рис.4 приведена схема использования счетчика фотонов на
телескопе. Как было отмечено, размер рабочей области фотокатода
ФЭУ-79 составляет несколько миллиметров, поэтому размер пятна
света на фотокатоде должен составлять также несколько
миллиметров. Перемещение пучка света при "дрожании" изображения
звезды или неточности наведения на звезду вызовет дополнительные
ошибки при измерениях, так как чувствительность фотокатода
неоднородна. Это можно избежать, если положение пятна на
фотокатоде не будет меняться при дрожании изображения звезды в
фокальной плоскости телескопа, т.е. в диафрагме электрофотометра.
Чтобы достигнуть этого, в электрофотометре применяется линза
Фабри, которая строит на фотокатоде изображение "неподвижного"
входного зрачка системы (т.е. объектива телескопа). Фокусное
расстояние линзы Фабри fлф выбирается так, чтобы диаметр
выходного зрачка , определяемый по формуле
d=fлф[ D/(F+a-fлф)] » fлф[ D/F] (здесь
a - расстояние от фокальной плоскости до линзы Фабри и обычно
a << F ), соответствовал размеру рабочей области фотокатода (как
правило, по уровню 0.8-0.9 максимальной чувствительности).
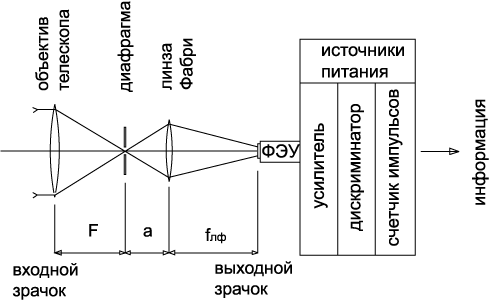
Рисунок 4: Схема использования счетчика фотонов на
телескопе
При наблюдении звезд с электрофотометром исследуемую звезду обычно
сравнивают с заранее подобранной звездой сравнения, звездная величина m0
которой известна. Если n* и n0 - частоты следования звездных импульсов при
наведении телескопа на одну и другую звезду, то свойство линейности ФЭУ
позволяет записать следующее уравнение для определения звездной величины
звезды:
Приходится учитывать, что в полное число регистрируемых за время T
импульсов N входит , помимо импульсов, рожденных "звездными" фотонами
N*,
импульсы, связанные со свечением неба рядом со звездой NH, и "темновые"
импульсы NT . Поэтому частота следования "звездных" импульсов равна
Рассмотрим от каких величин зависит точность оценки n*. Будем считать, что
число импульсов N*, Nн и Nт , регистрируемых за время T ,
распределено по времени
случайным образом. Статистическая флуктуация числа регистрируемых
импульсов при этом равна Ц{[`(N*,н,т)]}
где [`(N*,н,т)] - среднее число соответствующих
импульсов. Тогда ожидаемая флуктуация числа составит
Относительная точность измерения
Эта формула является основной при оценке статистической точности
измерений. Для ярких объектов (n* >> nH+nT) и
слабых объектов (n* << nH+nT) формула (3)
аппроксимируется простыми выражениями:
При оценке реальных возможностей фотометра и предполагаемой
точности измерений звезды, звездная величина которой примерно
известна, также используется формула (3); при этом учитывается,
что n*=hn*фот, а nH=hnHфот, где
h - квантовый выход ФЭУ (около 10%) , а
n*фот и nHфот - потоки фотонов, падающих на
фотокатод от звезды и от неба. Для практических расчетов полезно
помнить, что звезда нулевой звездной величины класса А0 дает в
фильтре V (зеленая область спектра) примерно 103 фотонов в
расчете на один ангстрем на каждый квадратный сантиметр площади
объектива, а одна квадратная секунда ночного неба соответствует
примерно 22-й звездной величине.
Порядок выполнения работы
Перед началом выполнения работы необходимо ознакомиться с основными
элементами установки. В комплект установки входят:
Подготовка к измерениям
Для снятия счетной и зонной характеристик ФЭУ требуется выполнить
следующие операции:
Примеры дополнительных вопросов к задаче
Литература
Основная:
Дополнительная:
|
| Вернуться к оглавлению |
| Перейти к следующей задаче |