| Вернуться к оглавлению |
| Перейти к следующей задаче |
|
Задача №09
СПЕКТРЫ И ПОКАЗАТЕЛИ ЦВЕТА
ЗВЕЗД
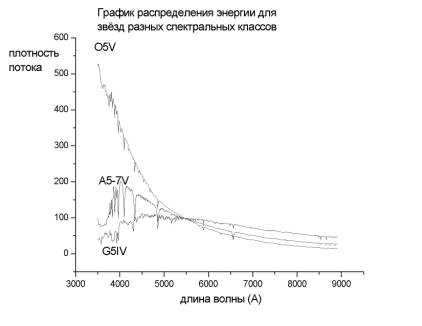
Целью задачи является знакомство с основными особенностями спектров звезд различных спектральных классов, с фотометрическими системами звездных величин и с определением показателей цвета по известному распределению интенсивности в спектре. Распределение энергии в спектрах звезд (форма спектра) зависит от многих факторов, и прежде всего - от эффективной температуры звезды, ее химического состава и селективного межзвездного ослабления света. В наблюдаемый спектр вносят свою лепту и искажения, вносимые атмосферой и оптикой телескопа. Их обычно учитывают путем сравнения измеряемых спектров со спектрами стандартных источников, форма которых считается известной. В настоящей работе будут рассматриваться спектры, присущие самой звезде. В качестве примера, на рис.1 приведен вид
спектров звезд различных классов.
Рис. 1 Даже если отвлечься от многочисленных
линий поглощения, спектры звезд имеют сложную форму, и довольно сильно
отличаются не только друг от друга, но и от спектров абсолютно черного тела
соответствующей температуры, что отражает отсутствие термодинамического
равновесия в тех слоях, где рождается принимаемое излучение. Звездные величины
и показатели цвета звезд чаще всего (хотя и не всегда) получают методом широкополосной фотометрии,
в которой используются фильтры с шириной от одной до нескольких тысяч ангстрем.
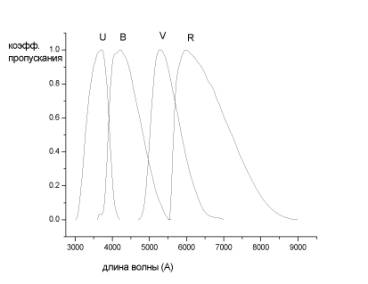
Из широкополосных систем звездных величин
наиболее распространена фотоэлектрическая система UBV, введенная в 50-е годы Джонсоном, и позднее продолженная в
инфракрасную область спектра (RIJHK). Каждая
фотометрическая полоса характеризуется своей функцией S(λ), которая может быть
приближенно описана двумя параметрами
– шириной полосы (эквивалентной шириной)
и эффективной длиной волны (см. [1]). Полосы UBVR относятся соответственно к ультрафиолетовой, голубой, визуальной,
и красной, а IJHK – к ближней инфракрасной областям спектра. На Рис. 2 приведены кривые
пропускания для фильтров UBVR.
Рис.2 Если F(λ) – плотность потока, приходящего
от звезды, а S(λ) – кривая реакция
фотометра (фильтр + приемник излучения)
, принятая в качестве стандартной для данной фотометрической системы, то
звездная величина в этой системе определяется как m = C – 2.5 lg ∫ F(λ) S(λ) dλ, (1) где интеграл формально берется от 0 до
∞, а постоянная С определяется через систему стандартных звезд, звездная
величина которых считается известной.
К сожалению, невозможно добиться полной тождественности S(λ) данной фотометрической полосы
для различных обсерваторий и условий наблюдений, поэтому при фотометрических
измерениях может возникнуть систематическая ошибка, различная для звезд с
разным распределением энергии в спектре.
Для ее исключения при сопоставлении измеряемой и стандартной звездной
величины звезд сравнения вводятся поправочные члены, зависящие от цвета звезды
(цветовые поправки). В качестве основного (первичного)
спектрофотометрического стандарта для звезд обычно используется самая яркая
звезда А0 – Вега. Распределение энергии в ее спектре считается известной
функцией. Фотометрические и спектральные наблюдения этой звезды позволяют
оценить как S(λ), так и
постоянную С в уравнении (1). Первичным эталонным источником, сравнение с
которым дает возможность провести абсолютную калибровку спектра звезды (в том
числе и Веги) на всех длинах волн, является модель абсолютно черного тела с
планковским спектром излучения, реализуемая в лабораторных условиях. Пусть индекс 1
относится к одной фотометрической полосе, а 2 – к другой (для определенности,
более коротковолновой). Тогда величиной, характеризующей цвет звезды в
интервале длин волн, охватываемых выбранными полосами, является показатель
цвета CI ≡ m2-m1 = (C2-C1) + 2.5( lg ∫ F(λ) S1(λ) dλ - lg ∫ F(λ) S2(λ) dλ) (2) Таким образом, каждая пара
фотометрических полос (U и B, B и V, V и R и т.д.) позволяет
определить свою шкалу показателей цвета. При этом для удобства сравнения
показателей цвета значение постоянной отсчета (С2-С1)
принимается таким, при котором для
близких звезд A0 (близких – чтобы на их цвете не
сказывалось межзвездное покраснение) все звездные величины оказываются
одинаковыми, то есть цвета для любой пары фотометрических полос для этих звезд
должен быть равным нулю. Этим условием определяется точка отсчета цветовых
шкал. Равенство нулю показателя цвета для звезды А0 запишется следующим
образом: (m2-m1)0 = (C2-C1)
+ 2.5( lg ∫ F0(λ) S1(λ) dλ - lg ∫ F0(λ) S2(λ) dλ) = 0. (3) В настоящей работе предлагается познакомиться с видом звездных спектров и
оценить показатели цвета звезд различных спектральных классов по известному
распределению энергии в спектре. Исходными
данными являются файлы с таблицами, дающими плотность потока как функцию длины волны. В задаче рекомендуется
использовать пакет программ для построения графиков Origin 4.1, хотя все математические операции могут быть проведены с применением самого различного
мат-обеспечения. Упражнение 1 Построение графика
зависимости потока от длины волны. При загрузке Origin открывается окно с незаполненной таблицей (worksheet).именно в таких таблицах будут производиться действия с нашими данными. Для того, чтобы открыть еще одно
окно нужно кликнуть в меню на «File-New- Worksheet» . На компьютере в директории d:\ Luda\ Spe\ (или в другой –
по указанию преподавателя) содержатся таблицы с распределением энергии для
звезд разных спектральных классов, а также с кривыми пропускания различных
фильтров(U1, B1, V1, R1).
Прежде всего, надо заполнить таблицу в «worksheet».
Для этого в меню выбрать « File - Import –ASCII» и скопировать в таблицу данные для спектрального класса звезды,
заданного преподавателем (например A1…3V). Для построения графика достаточно выбрать в меню: PLOT: LINE , обозначить A(X)
- X, а
B(Y) -Y и получить график на экране. По горизонтальной оси –длины волн в
ангстремах (1А = 10-10 м), по вертикальной – плотность потока Fl(l) в расчете на
единичный интервал длин волн (с точностью до произвольного множителя). По указанию преподавателя график можно
отправить на принтер. На записи требуется отождествить основные
линии в спектре звезды. Упражнение 2. Сравнение спектра звезды со спектром абсолютно черного
тела. Спектры большинства звезд могут быть с некоторой точностью (часто – очень
грубо) представлены спектром абсолютно черного тела на определенном интервале
длин волн: FBl (T) = cоnst×/l5×exp(hс/klT-1). (4) Максимум спектра
достигается на lmax = 0.29/T [cm], а максимальное значение
FBl (T)max =
сonst×T5
(5) Для сравнения FBl (T) и Fl необходимо
на-глаз оценить положение lmax , определить из (5) значение T, при котором спектр абсолютно черного тела имеет
максимум на той же длине волны, и, проведя простые вычисления, найти величину const в формуле
(4) из условия совпадения этих двух
функций на l =lmax. После этого надо создать и активизировать незаполненную колонку в worksheet, и с помощью опций «column – set column values» ввести
математическое выражение для счета по формуле (4) с использованием найденной
константы. Нажатием на «DO IT» функция FBl (T) записывается
в форме таблицы. В графическом окне
изображаются обе сравниваемые функции, которые должны иметь общую точку на l = lmax. График надо записать. Упражнение 3. Интегрирование
спектра по длинам волн. Преподавателем должны быть указаны две
выбранных фотометрических полосы. Для каждой из них необходимо подсчитать поток
излучения через соответствующий фильтр (формула (1)), перемножив коэффициенты пропускания каждого
фильтра, и значения потоков для тех же длин волн. К примеру, пусть надо перемножить
колонки B(Y) в Worksheet A1…3V (или другом, для
звезды другого класса), где содержатся значения плотности потоков, и B(Y) во втором открытом окне (Worksheet b1) с данными о кривой пропускания S(l) для выбранного фильтра. Перемножение можно производить как в
пустом Worksheet , так и в уже
используемом. Ниже мы опишем
перемножение в пустом Worksheet. Используя «File – New – Worksheet», в пустой
Worksheet
копируем нужные колонки из B1. и A1…3V. Затем:
а) увеличиваем число
колонок : Column - Add New Columns,
б) активизируем col. A(x) в Worksheet B1 - Edit – Copy
, активизируем col.
A(x) в пустом Worksheet -
Edit - Past, в) повторяем
для col. B(Y) , г) из Worksheet
A1…3V копируем col. B(Y) , следя за соответствием длин волн,
д) активизируем col. D(Y)
и перемножим колонки :
кликнем
Column – Set Column Values, внесем необходимые изменения. Для построения графика повторяем
операции из упр.1 Чтобы
получить поток, проинтегрированный по длинам волн, посчитаем интеграл
∫F(λ) S(λ) dl. Это достигается путем использования опций
«Analysis – Calculus – Integrate». Результат записывается, и все операции
повторяются для другого фильтра. В итоге имеем два подсчитанных интеграла. Для полос B и V их можно обозначить как FB
и FV . Их отношение и
будет характеризовать цвет звезды, но для получения оценки показателя цвета его
необходимо сравнить с аналогичным отношением для звезд А0. Упражнение 4. Оценка показателя цвета звезды Описанные
в предыдущем упражнении операции с теми же двумя фильтрами повторяем для звезды А0, показатель цвета
которой по определению равен нулю. В итоге для этой звезды будут получены
значения интегралов F01 F02. Следуя (1-3), имеем: m2-m1 = 2.5×(lg F1 /F2
– lg F01/F02). Это значение и является результатом
оценки показателя цвета звезды данного спектрального класса. Что надо знать до начала выполнения задачи
Примеры контрольных вопросов
Литература
|
| Вернуться к оглавлению |
| Перейти к следующей задаче |