| Вернуться к оглавлению |
| Перейти к следующей главе |
|
|
Итак, мы убедились, что излучение
в некоторых условиях проявляет корпускулярные свойства. С другой стороны, дифракционная
картина, наблюдаемая при рассеянии на кристаллах различных частиц — электронов,
нейтронов и целых атомов — свидетельствует в пользу их волновой природы. Как
совместить волновые и корпускулярные свойства объектов микромира? Ведь частица локализована
в пространстве, а волна представляет собой протяжённое образование. Например,
монохроматическая волна заполняет собой всё пространство и вопрос о её
местонахождении лишён смысла. Тем не менее, волновой процесс можно локализовать.
Для этого надо создать волновой пакет — сумму многих колебаний с разными
частотами и длинами волн. 6.1 Фазовая скорость
Запишем уравнение монохроматической
волны, распространяющейся в положительном направлении оси x: Y(x,t) = A cos(kx–w t), где Y —
любая физическая величина, описывающая волновое движение. Аргумент
гармонической функции (в данном случае
— косинуса) называется
фазой: j
= kx – w t. Выразим координату через фазу и время: Если мы зафиксируем фазу, то координата становится линейной
функцией времени. Такая зависимость называется характеристикой. На рисунке 6.1.1
показаны три характеристики, 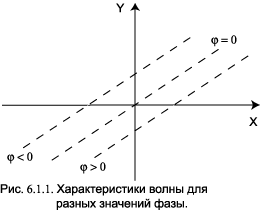
отвечающие различным значениям фазы. Множитель перед t называется фазовой скоростью волны: Физический смысл фазовой скорости заключается в следующем. Для наблюдателя, который движется со скоростью Vф в направлении распространения волны, величина Y становится постоянной и волна как бы застывает. Однако, во многих случаях оказывается, что фазовая скорость волны больше скорости света. Здесь нет никаких противоречий, так как темп переноса энергии описывается совсем другой характеристикой волнового пакета. 6.2 Групповая скоростьПонятие групповой скорости связано с интерференцией колебаний, имеющих разные частоты и длины волн. Рассмотрим две волны с одинаковыми амплитудами и различающимися, но близкими частотами и длинами волн: причём Сложим эти колебания: В аргументе первого косинуса правой части мы пренебрегли слагаемыми Δω и Dk по сравнению с 2w и 2k. На рис.6.2.1 приведён график функции Y(x) в некоторый момент времени. Результирующее 
колебание представляет собой волну практически с прежними
значениями частоты и волнового числа, но с модулированной амплитудой. Мы можем
добиться того, чтобы для нас стала неподвижной картина модуляции амплитуды. Для
этого надо двигаться со скоростью До сих пор мы рассматривали одномерный случай. На рис.6.2.2
представлена имитация сложения волн, распространяющихся в разных направлениях
на плоскости. Из равноотстоящих точек под разными углами проведено по пять
линий. Хорошо видно, как они образуют периодические сгущения и разрежения по обоим направлениям. 
Если сложить большое число волн, то получится более сложная картина биений с большей степенью локализации колебаний, но элементы периодической структуру будут многократно повторяться. Этот результат пока ещё отличается от наших представлений о частице, находящейся в определённой области пространства. Локализацию волнового пакета можно получить только при непрерывном распределении частот и волновых чисел. Тогда частоту можно представить как непрерывную функцию волнового вектора: (2.2) w = w (k). Зависимость (2.2) называется дисперсионным уравнением. Именно для такой функции вводится понятие групповой скорости как предела (2.1): Групповая скорость есть скорость передачи любого сигнала, а также скорость переноса энергии, массы и аналогичных величин. Она никогда не превосходит скорости света в вакууме. 6.3 Сложение колебаний с непрерывной зависимостью w(k)
При непрерывной зависимости (2.1)
волновой пакет должен быть представлен не в виде суммы, а как интеграл от
непрерывного распределения монохроматических колебаний: 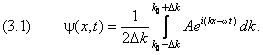
причём Dk = k0. Здесь для удобства дальнейших вычислений мы перешли к экспоненциальному
представлению колебаний и добавили «нормировочный» множитель 1/(2 Dk). Амплитуда A, вообще говоря, может зависеть от
волнового числа k,
но мы для простоты будем полагать её постоянной и вынесем за знак интеграла. Рассмотрим модуляцию колебаний в
пакете волн с непрерывным распределением частот, ограничиваясь линейным
разложением по малому параметру Dk
= k – k0: где Подставив (3.2–3) в (3.1) и выполняя интегрирование,
получим: 
Мы снова пришли к уравнению для плоской волны с частотой w0 и волновым числом k0,
но с модулированной амплитудой. На этот раз модуляция осуществляется функцией график которой приведён на рис.6.3.1. Нам важны следующие её свойства. Во–первых, функция f(x) 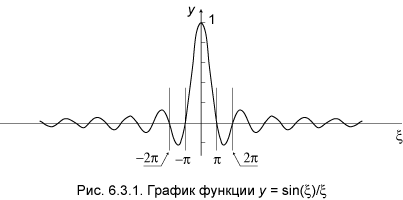
принимает наибольшее значение в центре волнового пакета: f(0)
= 1. Далее, вместе с sinx она
имеет бесконечное число корней: f(x) = 0 при x = ±
p n
n = 1, 2,¼ Наконец, в промежутках между нулями, в точках x = p/2 ± p n n = 1, 2,… модуль функции имеет локальные максимумы, высота которых падает обратно пропорционально x. Модулированный пакет (3.4) изображён на рис.6.3.2: он практически полностью локализован в 
первом максимуме. Чёрная кривая
изображает колебания на основной частоте w0. Им
соответствует фазовая скорость Vф
» w0/k0 . (Напомним, что мы полагаем |Dk| и |Dw| малыми по сравнению с k и w, соответственно). Красным цветом обозначена
огибающая волнового пакета. Она перемещается в пространстве с групповой
скоростью Vг0, определяемой формулой (3.3). 6.4 Локализация пакета и его длительность
Фиксируем момент времени t = 0. Тогда аргумент
функции амплитудной модуляции равен x = x× Dk. График функции на рис. 6.3.2 в данном случае представляет мгновенную фотографию волнового пакета. Повторим центральную часть рис. 6.3.1 с новыми обозначениями.
Размер пакета определяется шириной центрального максимума,
где фаза x меняется
на 2p: (4.1) Dk Dx … 2p. Знак неравенства напоминает, что часть пакета, хотя и небольшая,
всё же выходит за пределы центрального максимума. Теперь оценим, сколько времени волновой пакет тратит на прохождение через заданную точку, например, через начало координат. В этом случае x
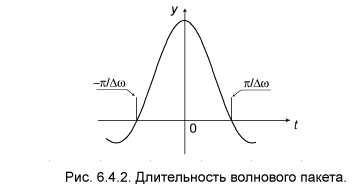
= – Vг0× t Dk= – Dw×t. Однозначную зависимость функции f(x) от времени отражает рис. 6.4.2.
Длительность волнового пакета, как и пространственная протяжённость,
определяется изменением фазы на 2p: (4.2) Dw×Dt … 2p. Неравенства (4.1) и (4.2) хорошо известны в теории колебаний
и в радиотехнике. Например, так называемая почти
монохроматическая волна (волновой пакет с очень узким интервалом волновых чисел)
имеет большую протяжённость в пространстве. С другой стороны, для регистрации
коротких (Dt → 0)
импульсов необходим широкополосный приёмник. Рассматриваемые неравенства
отражают операции, необходимые для измерения длины волны l
и частоты. Для определения λ необходимо фиксировать положения как минимум
двух соседних «горбов». При этом точность определения l
будет тем больше (Dl →
0 и Dk → 0), чем большее число максимумов будет зафиксировано (Dx → ¥).
Аналогично, для определения частоты колебаний маятника w измерение нужно проводить,
по крайней мере, в течение одного периода колебаний. Точность измерения частоты
будет возрастать (Dw
→ 0) с увеличением числа измеренных периодов (Dt → ¥). 6.5 Частица как волновой пакет
Итак, мы можем представить материальную частицу как волновой пакет. Вычислим фазовую и групповую скорости такого пакета, для определённости задавшись параметрами электрона. Припишем частице частоту, соответствующую дебройлевской длине волны. В результате фазовая скорость получается равной Воспользуемся формулами (1.2) четвёртой главы, выражающими импульс и энергию через скорость V, и продолжим цепочку равенств: Последнее неравенство еще раз убеждает нас, что фазовая скорость не имеет прямого отношения к скорости частицы. Теперь определим групповую скорость частицы как волнового пакета: Вычисление производной dE/dp можно выполнить следующим образом. Из формул (1.2) четвёртой главы вытекает полезное тождество, объединяющее скорость, импульс и энергию частицы: (5.3) E = pc2/V. Воспользуемся (5.3) и продолжим цепочку равенств (5.2): Скорость перемещения огибающей волнового пакета есть скорость
движения частицы. 6.6 Линейная и нелинейная дисперсионные зависимостиВ случае линейной связи между частотой и волновым числом фазовая скорость равна групповой. Например, электромагнитные волны в вакууме, как известно, описываются линейным уравнением w = kc. Их него следует Vф = Vг
= с. Но при распространении в той или иной среде связь между
частотой и волновым числом может оказаться нелинейной. Принято говорить, что
такая среда обладает дисперсией. При нелинейной функции w(k) групповая
и фазовая скорости различаются. Например, распространение электромагнитной
волны в плазме описывается дисперсионным уравнением где w0
— плазменная частота. Она определена формулой (1.2.1) в разделе 1.1.2 (Ленгмюровская частота) первой главы (Анализ размерностей). Дифференцируя
(6.1) по волновому числу k, получаем: 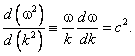
Из последнего равенства вытекает связь между фазовой и групповой скоростями электромагнитной волны в плазме: Vф
× Vг = с2. Сами скорости в единицах скорости света равны 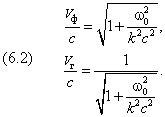
Таким образом, фазовая скорость получилась больше скорости
света, а групповая скорость — меньше c, в полном соответствии с её смыслом как скорости передачи
сигнала. 6.7. Расплывание волнового пакета
Поскольку волновой пакет состоит
из волн с различающимися фазовыми скоростями, то эти волны с течением времени
должны расходиться, а волновой пакет — расплываться. Время расплывания пакета
можно оценить, удержав в разложении (3.2) слагаемое со второй производной d2w /dk2: Теперь показатель экспоненты в формуле (3.1) равен где
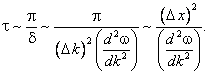
Здесь мы воспользовались соотношением (4.1), которое связывает протяжённость волнового пакета с разбросом волновых чисел. Квадратичное слагаемое равно нулю при линейной зависимости частоты от волнового вектора. В этом случае эффект расплывания волнового пакета не имеет места, как, например у фотона в вакууме. Рассмотрим теперь нерелятивистску частицу
с массой M. Вторую производную частоты по волновому
вектору оценим следующим образом: Следовательно, время расплывания волнового пакета по порядку
величины составляет В классическом пределе (h
→ 0) эффект расплывания отсутствует. Примеры
Пусть макроскопическое тело имеет массу M = 1г и размер Dx ~ 1 м (дробинка). Тогда из (7.1) получаем
t
~ 1018 лет. Это значительно превышает возраст Вселенной. Таким
образом, объекты макромира не успевают расплыться за время своего существования. Перейдём к объектам микромира.
Формула (7.1) упрощается в случае электрона.
Если M=me, то te ~ (D x)2 при условии, что расстояние измеряется в сантиметрах, а время
— в секундах. Проверим, может ли электрон удержаться внутри области, размер
которой равен его классическому радиусу
re.
В этом случае te ~ re2 ~ t ~ 10–26 с. Электрон практически мгновенно «уплывет» в другое место. Классический
радиус электрона численно близок к размерам ядра. Следовательно, мы показали
также, что электрона в ядре быть не может. Атомный электрон локализован внутри области Dx ~ a0 ~ 10–8 см, откуда время
расплывания 10–16 с
оказывается сравнимым с периодом обращения электрона
на орбите вокруг ядра. Мы рассмотрели два примера
поведения микрочастицы на микроскопических расстояниях. Теперь обсудим движение
электрона в масштабах домашнего телевизора и околоземной орбиты. Электрон в кинескопе телевизора, пройдя разность потенциалов ~ 20 кэВ, разгоняется до скорости ~ 1010 см/с. Пусть чёткость
изображения удовлетворительна при его локализации на экране с точностью до Dx ~ 0.1 мм. Если размер пакета
принять равным этой величине, то время расплывания получается равным 10–4 с. За это время электрон пролетит
10 км — расстояние, значительно превышающее размер телевизора. Итак, в
трубке кинескопа не происходит расплывания электрона как волнового пакета. Космофизичекий эксперимент. В советско–французском
эксперименте под кодовым названием «Аракс» с острова Кергелен
в Южном полушарии вблизи северного магнитного полюса запускалась в атмосферу
ракета с электронной пушкой, которая инжектировала в атмосферу пучок электронов
с энергией примерно 10 кэВ. Электроны летели вдоль силовых линий
магнитного поля Земли и были зарегистрированы в районе Архангельска. Длина пути
была около 109 см. При скорости 1010 см/с такое
расстояние электрон проходит примерно за десятую долю секунды. Отсюда следует
величина расплывания пакета порядка нескольких миллиметров — в 109
раз меньше длины пути электрона. Таким образом, в случае микроскопической
частицы, двигающейся в макроскопических масштабах, расплывания волнового пакета
не происходит. Итак, расплывание волнового
пакета может оказаться существенным только при движении микроскопической
частицы в микроскопических масштабах, то есть там, где законы классической
механики уже неприменимы. |
| Вернуться к оглавлению |
| Перейти к следующей главе |

 Квадратичная
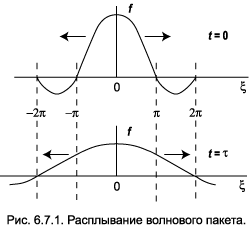
добавка даёт дополнительный набег фазы. Сказанное иллюстрирует рис. 6.7.1.Будем
полагать, что произошло заметное расплывание, если за промежуток времени
Квадратичная
добавка даёт дополнительный набег фазы. Сказанное иллюстрирует рис. 6.7.1.Будем
полагать, что произошло заметное расплывание, если за промежуток времени