Особое место занимают задачи, в которых потенциальная энергия зависит только координат:

Такие состояния называются стационарными, так как в них сохраняется энергия системы E. Отсутствие явной зависимости гамильтониана от времени позволяет выполнить разделение переменных. Волновую функцию ищем в виде произведения

Множитель f(t) отражает волновую природу частиц в квантовой теории. Мы в этом убедимся, когда выведем для него явное выражение. Подставим (1) в уравнение Шредингера (8.1.8):

 

и разделим обе части равенства на произведение

Левая часть зависит лишь от времени, а правая — только от пространственных координат. Следовательно, они обе равны одной и той же константе:

 

 

Легко убедиться, что константа имеет размерность энергии. Таким образом, имеем два уравнения

причём второе показывает, что константа разделения E действительно равна энергии системы. Зависимость волновой функции от времени получаем из (2a):

Итак, временнóй множитель стационарного состояния является осциллирующей функцией. Энергии E соответствует частота . Следовательно, формула (3) в той же мере описывает состояние с энергией E, как  — колебания на частоте w.

Пространственная часть волновой функции удовлетворяет уравнению (2b), которое с учётом выражения (1.7) восьмой главы для оператора Гамильтона можно переписать как:

 

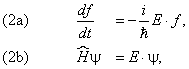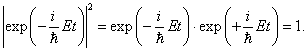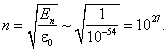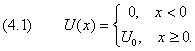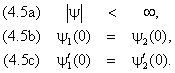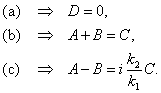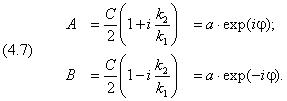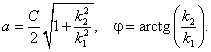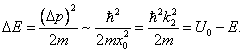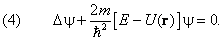
Мы получили стационарное уравнение Шредингера. Полная волновая функция имеет вид

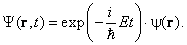
Плотность вероятности в стационарном случае не зависит от времени. В самом деле, квадрат модуля временнóго множителя (3) равен единице:

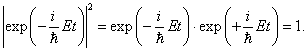
Следовательно, вероятность W найти частицу в той или иной точке пространства (формула (2.1) восьмой главы) определяется исключительно координатной частью волновой функции:

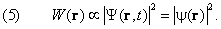
Формула (5) окончательно проясняет смысл функции f(t). Последняя описывает волновые свойства стационарного состояния, но никак не влияет на местоположение частицы.

В одномерном случае (4) сводится к обыкновенному дифференциальному уравнению второго порядка

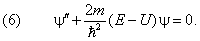
Штрихом для краткости обозначен оператор дифференцирования по единственной пространственной координате x:

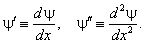
В дальнейшем мы рассмотрим несколько задач для простейших одномерных потенциалов.

9.1 Свободная частица

Решим уравнение (6) предполагая отсутствие внешних полей, то есть, при равном нулю потенциале U:

 

Обозначив

получаем уравнение гармонической функции

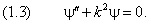
Его два линейно независимых решения равны:

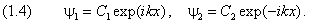
Далее, введём частоту

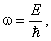
и перепишем временнýю часть волновой функции в виде

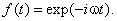
Полная волновая функция равна

 

 

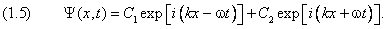
Таким образом, решением уравнения (1.1) являются две плоские волны, распространяющиеся в противоположные стороны. Мы снова вернулись к связи между свободной частицей и монохроматической волной.

Формула (1.5) иллюстрирует важное свойство микромира. А именно, одному значению энергии может соответствовать несколько различных квантовых состояний. Такие уровни энергии принято называть вырожденными, а число квантовых состояний — степенью вырождения, или статистическим весом. В данном случае статистический вес равен двум, соответственно числу возможных направлений движения волны. Явление вырождения является типичным для квантовой механики.

В случае одномерного движения вырождение определяется именно возможностью частице свободно двигаться в обоих направлениях. Покажем, что если её движение ограничено хотя бы с одной стороны, то вырождение исчезает.

9.2. Одномерное движение, ограниченное с одной стороны.

Поставим вопрос, насколько могут различаться волновые функции y₁ и y₂, являющиеся решением уравнения (6), если они соответствуют одному и тому же уровню энергии E. Предполагается, что частица может неограниченно удаляться только в одном из двух направлений по оси x. Покажем, что при выполнении этого условия обе функции описывают одно и то же квантовое состояние. Поскольку они удовлетворяют уравнению (6), мы можем записать

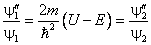
или

(2.1)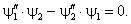   

В последнем равенстве прибавим и вычтем произведение 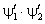. После этого становится ясно, что (2.1) является производной следующего уравнения:

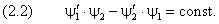
Теперь воспользуемся условием частичной ограниченности движения. В направлении, куда частица не имеет права двигаться неограниченно, обе волновые функции на бесконечности исчезают. Следовательно, константа в правой части (2.1) равна нулю, и справедливо равенство

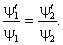
После повторного интегрирования получим

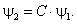
Согласно пункту «Принцип суперпозиции» раздела 2.1 восьмой главы, волновые функции, различающиеся лишь постоянным множителем, описывают одно и то же состояние.

Итак, вырождение отсутствует, если движение частицы вдоль прямой ограничено хотя бы с одной стороны.

9.3 Частица в потенциальном ящике

 

Рассмотрим задачу о прямоугольной потенциальной яме с бесконечно высокими стенками. На рис.9.3.1 ей соответствует потенциал следующего вида: В промежутке 0 < x < L он равен

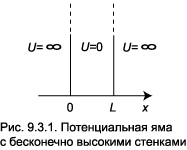
нулю и частица там движется свободно, а за пределами этого интервала (x < 0 и x > L) потенциал равен бесконечности. В области 0 ≤ x ≤ L уравнение Шредингера сводится к (1.1). В задаче о свободной частице мы получили осциллирующие решения (1.4), которые записали в виде экспоненты с мнимыми показателями ±ikx. Сейчас нам удобнее перейти к эквивалентному представлению, содержащему синус и косинус:

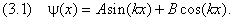
Константы A, B и k найдём из граничных условий и нормировки волновой функции. На стенках волновая функция обращается в нуль, так как в силу бесконечности потенциала частица не может выйти за пределы интервала 0 ≤ x ≤ L. Первое граничное условие даёт

что позволяет уточнить (3.1):

 

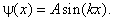
Второе условие

 

 

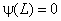
накладывает ограничения на величину волнового числа частицы. В самом деле, из уравнения

 

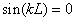
вытекает

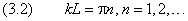
Обратим внимание на то, что параметр n не принимает нулевого значения, так как в этом случае волновая функция повсюду равна нулю, что означает отсутствие частицы в ящике. Таким образом, мы получили решение

 

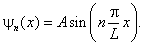
Константу A найдём из условия нормировки (8.2.7):

 

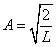
для любого n. Итак, нормированная волновая функция n–го состояния равна

 

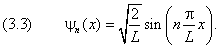
Собственному вектору задачи (3.3), согласно (3.2) и (1.2), соответствует собственное значение энергии

 

 

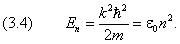
где

.

 

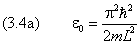Мы получили дискретный энергетический спектр, иными словами — квантование энергии. Состояние, в котором частица имеет самое низкое из всех возможных значение энергии, принято называть основным. В рассматриваемой задаче основное состояние отвечает значению n = 1. Остальные уровни энергии называют возбуждёнными.

Энергия частицы в потенциальном ящике не может принимать нулевого значения:

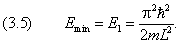
Этот факт имеет чисто квантовую природу. Действительно, если мы локализуем частицу на отрезке длиной L:

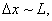
то, согласно соотношению неопределенностей Гайзенберга, она имеет импульс

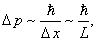
а, следовательно, её минимальная энергия составит

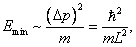
что с точностью до численного множителя совпадает с величиной 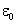. Мы лишний раз убедились, что заключённая внутри атома частица микроскопической массы не может находиться в состоянии покоя.

Формулы (3.3) и (3.4) показывают, что волновая функция однозначно определяется значением энергии. Таким образом, в данном случае вырождение не имеет места, в согласии с общим результатом, полученным в предыдущем разделе.

На рис.9.3.2 изображены волновая функция y(x) (слева) и вероятность W(x) (справа) для

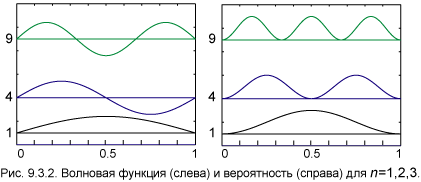
трёх первых значений n = 1, 2, 3. По горизонтальной оси отложено отношение x/L. Чёрным цветом обозначено основное состояние, синим — n = 2 и зелёным — n = 3. Прямые линии параллельные оси x (1, 4 и 9) отмечают значение энергии. В тех точках, где волновая функция обращается в нуль, частица никогда не будет обнаружена. Нулям функции W(x) нет аналогии в классической механике, но им соответствуют узлы стоячих волн в теории колебаний.

Подсчитаем число узлов волновой функции. Функция, описывающая основное состояние частицы, обращается в нуль только на концах интервала, а внутри него она узлов не имеет. В первом возбуждённом состоянии волновая функция имеет ровно один корень внутри отрезка (0, L), во втором — два и так далее. Здесь проявляются общие закономерности одномерного движения.

В математике известна так называемая осцилляционная теорема, справедливая для дискретного спектра энергии. Она связывает друг с другом номер собственного значения и число узлов волновой функции. Перенумеруем собственные значения оператора с помощью числа n, принимающего следующий ряд значений:

n = 0, 1, 2, 3, …

Функция ψ_n(x), соответствующая собственному значению E_n, при конечных значениях аргумента обращается в нуль ровно n раз. Если, как в рассматриваемой задаче, частица может находиться только на ограниченном отрезке оси x, то речь идёт о нулях функции ψ_n(x) внутри этого отрезка. Волновая функция основного состояния (n = 0) узлов не имеет.

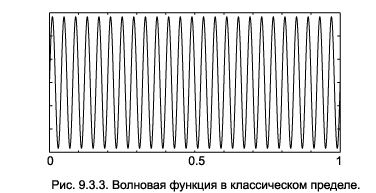
Плотность вероятности, соответствующая очень большим значениям n, быстро осциллирует (рис.9.3.3). В случае прибора с конечной разрешающей способностью в его апертуру попадает много пиков, и мы таких осцилляций не обнаружим. Так квантовая механика переходит в классическую.

Длина волны де Бройля

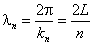
в классическом пределе n>>1 значительно меньше размеров системы L. Это случай геометрической оптики (классической механики), когда волновыми свойствами частицы можно пренебречь. Квантование энергии при этом тоже становится незаметным. Разность энергий 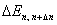между уровнями с номерами n и Δn при больших значениях n может быть вычислена с помощью производной функции (3.4) по n:

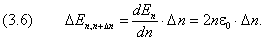
При увеличении квантового числа n энергетическая щель между двумя соседними уровнями (Δn = 1) растёт медленнее, чем энергия уровней:

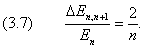
Таким образом, сильно возбуждённые состояния в классическом пределе (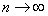) практически сливаются друг с другом и образуют спектр, близкий к непрерывному.

Некоторые примеры

Рассмотрим различные варианты движения частицы, меняя её массу и область локализации.

1.                  Макроскопическая частица в макроскопических масштабах: m = 1г, L = 1см. Для неё

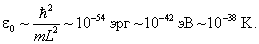
Такую величину измерить невозможно. Оценим номер уровня при скорости движения V = 1 см/с. Кинетическая энергия ~ mV² составляет около 1 эрг. Отсюда, согласно (3.4),

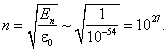
Энергетическая щель (3.7) между соседними уровнями составляет

 

(3.8)                 ΔE_n,n+1 ~ 10^–27 эрг ~ 10^– 15 эВ ~ 10^–11 K.

 

Она также слишком мала, чтобы её можно было обнаружить. Таким образом, макроскопическая частица находится на очень высоком квантовом уровне, а расстояние между соседними уровнями настолько мало, что квантовых свойств мы наблюдать не будем. Поэтому энергетический спектр является практически непрерывным, в соответствии с (3.7).

2.                  Электрон в макроскопических масштабах длин: m ~ 10^–27 г, L ~ 1 см. Его энергетический спектр почти совпадает с (3.8).

3.                  Электрон в атоме: L ~ 10^–8 см. В этом случае квант энергии по порядку величины равен

                        e₀ ~ 10^–11 эрг ~ 10 эВ ~ 10^–11 K

 

оказывается вполне сравнимым с оценкой энергии основного состояния атома (1.2.5).

Итак, дискретность энергетического спектра заметна только для микроскопических частиц в микроскопических масштабах. Энергия макроскопических частиц на любых масштабах, а также микрочастиц в макроскопических масштабах имеет спектр, практически неотличимый от непрерывного.

9.4 Потенциальный порог

Согласно классической механике, частица, налетая на потенциальный порог, проскакивает его, если её энергия достаточно велика. В противном случае она отражается от барьера.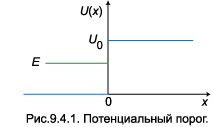

В квантовой механике ситуация сложнее. На рис.9.4.1 график потенциальной энергии U(x) изображён синей линией. Функция U(x) обращается в нуль в области отрицательных значений аргумента и равна постоянной величине U₀ для x ≥ 0:

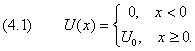
В точке x = 0 потенциальная энергия терпит разрыв. Энергия налетающей частицы E помечена зелёным цветом. В этом разделе мы будем считать, что энергия частицы меньше потенциального барьера:

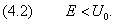
В классической механике такое неравенство означает отражение частицы. Переходим к решению уравнения Шредингера. Для отрицательных значений аргумента оно записывается как

 

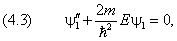
а в области x ≥ 0 имеет вид

 

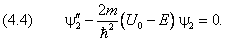
Решение этих уравнений должно удовлетворять следующим условиям:

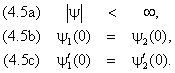
Условие (4.5a) означает ограниченность волновой функции. Оно вытекает из того, что вероятность |y|² обнаружить частицу в той или иной точке пространства должна быть конечной величиной. Требование непрерывности волновой функции (4.5b) отражает отсутствие процессов рождения и аннигиляции частиц. Непрерывность первой производной является следствием ограниченности потенциала. Для вывода (4.5c) уединим вторую производную в левой части уравнения Шредингера (6):

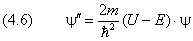
Если все величины в правой части ограничены:

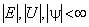
то из (4.6) следует ограниченность второй производной волновой функции. Отсюда, в свою очередь, вытекает непрерывность . В предыдущем разделе потенциал на краях интервала 0 ≤ x L обращался в бесконечность (рис. 9.3.1). Именно там первая производная  терпит разрывы, приводящие к изломам волновой функции в точках 0 и L.

Приступим к решению задачи. Введём волновые числа

 

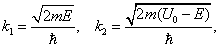
с которыми уравнения (4.3) и (4.4) преобразуются в

 

 

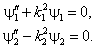
Первое уравнение имеет осциллирующие решения, аналогичные (3.1). Но сейчас нам удобнее перейти к их экспоненциальному представлению с мнимой единицей:

 

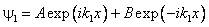
Решение второго уравнения — линейная комбинация убывающей и растущей экспонент:

 

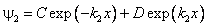
Граничные условия (4.5) дают три уравнения:

 

 

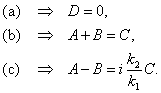
С их помощью константы A и B могут быть выражены через C:

 

 

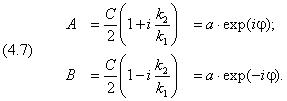
Мы ввели обозначения

 

 

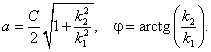
Таким образом, в области x < 0, где движение разрешено и в классической механике, получаем осциллирующее решение

 

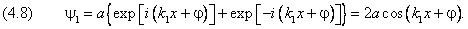
Оно представляет сложение двух волн равной амплитуды. Первое слагаемое описывает падающую волну, второе — отражённую, их сумма — стоячую волну.

Перейдём к области x > 0, запрещённой для движения классической частицы. Константу C удобно выразить через параметры a и j:

 

 

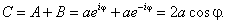
Решением здесь является экспоненциально затухающая функция

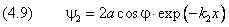
На расстоянии x₀ = 1/k₂ она убывает в e раз. Соответственно, вероятность обнаружить частицу на расстоянии x₀ от порога равна |Ψ₂|² ≈ 0.1. Рис. 9.4.2 иллюстрирует полученное решение. Потенциальный барьер помечен синим цветом. Слева от границы барьера осциллирующая часть волновой функции Ψ₁ изображена зелёной кривой, а красная линия справа обозначает экспоненциально затухающую функцию Ψ₂. Пунктиром показана касательная к волновой функции в

 

 

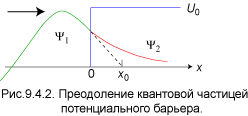
начале координат. Она пересекает горизонтальную ось в точке x = x₀.

Формула (4.9) показывает, что квантовая частица может проникать сквозь потенциальный барьер даже в том случае, когда её энергия E меньше его высоты U₀. В пределе классической физики величина x₀ стремится к нулю вместе с постоянной Планка:

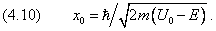
Чем больше энергия E частицы, тем дальше проникает она в классически запрещённую область движения. Если мы будем увеличивать энергию E, приближая её к U₀, то, согласно (4.10), величина x₀ неограниченно растёт. Это соответствует классическим представлениям о том, что частица с энергией E ≥ U₀ должна беспрепятственно проходить потенциальный барьер. Схематически

 

 

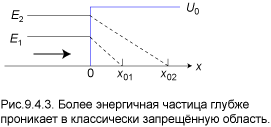
зависимость x₀ от E представлена на рис. 9.4.3.

Попробуем обнаружить частицу в окрестности точки x₀, например, «подсветив» её фотоном. Частица будет локализована в пространстве с точностью

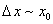
Согласно соотношению неопределённостей Гайзенберга, мы сообщим ей импульс

 

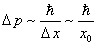
то есть, частица приобретает дополнительную энергию

 

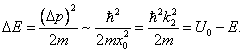
позволяющую преодолеть потенциальный барьер. Таким образом, «подсвеченную» частицу можно обнаружить в области, недоступной для классического движения; но её энергия окажется выше пороговой.