| Вернуться к оглавлению |
| Перейти к следующей главе |
|
|
Теория Бора, изложенная в предыдущей главе, отождествляет дискретное состояние атома с энергетическим уровнем. В действительности атом, как всякая квантовая система, может находиться в различных состояниях с одним и тем же значением энергии. С такой ситуацией, называемой вырождением, мы уже познакомились в девятой главе, рассматривая одномерное движение свободной частицы. Вырождение заключалось в том, что частица может двигаться с одной и той же скоростью в двух противоположных направлениях. Правда, там же показано отсутствие вырождения в случае ограниченного одномерного движения. Действительно, в задачах о движении частицы в потенциальной яме и её отражения от потенциального барьера вырождение не имело место. Но вращение электрона вокруг ядра не является одномерным, и это в корне меняет ситуацию: состояния атома могут быть вырождены, несмотря на то, что движение связанного электрона в нём ограничено. Напомним некоторые определения: число разных состояний, принадлежащих одному уровню энергии, называется степенью вырождения, или статистическим весом, а также просто весом уровня. Таким образом, необходимо различать квантовые состояния и энергетические уровни атомов. В модели круговых орбит вырождение отсутствует, так как, согласно (13.3.7), момент вращения электрона однозначно выражается через его энергию. Интерпретация вырождения в рамках модели Бора была предложена Зоммерфельдом: он ввёл представление о плоских эллиптических орбитах и о пространственном квантовании. В классической механике большая полуось эллипса однозначно связана с энергией движения, в то время как его форма определяется также и моментом вращения. Следовательно, одной и той же энергии при движении по эллипсу могут отвечать разные значения момента. В квантовой теории это свойство классического движения проявляется как вырождение. Перейдём к количественному изложению теории Бора–Зоммерфельда 15.1. Эллиптические орбитыИзвестно, что механическая система с k степенями свободы описывается с помощью k обобщённых координат qi(i = 1, 2, …, k) и соответствующих им обобщённых моментов 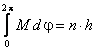 .
Отсюда следует (13.1.1). Обратим
внимание на применение двух обозначений для одной и той же величины — квантового
числа момента вращения. В главе 12, где исследуются квантовые свойства
орбитального момента, мы пользовались буквой l. Но в
классической механике момент имеет иные свойства. Поэтому мы приняли разные
обозначения для двух аспектов момента: .
Отсюда следует (13.1.1). Обратим
внимание на применение двух обозначений для одной и той же величины — квантового
числа момента вращения. В главе 12, где исследуются квантовые свойства
орбитального момента, мы пользовались буквой l. Но в
классической механике момент имеет иные свойства. Поэтому мы приняли разные
обозначения для двух аспектов момента:
Из аналитической геометрии известно уравнение эллипса с большой полуосью a и эксцентриситетом ε: Вычислим обобщённый момент pr, соответствующий радиальной координате: и запишем второе условие стационарности: 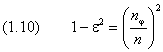 , ,
где введено обозначение 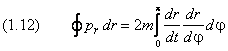 . .
В записи то есть, двум значениям угла φ отвечает одно и то же расстояние r. Во время движения электрона по эллипсу приращение dr в точке 2π – φ имеет другой знак, чем в точке φ: dr(2π–φ) = –dr(φ) при тех же самых изменениях dt и dφ. Вместе с dr становятся отрицательными обе производные: dr/dt и dr/dφ. Следовательно, подынтегральная функция в правой части (1.12) сохраняет своё значение при зеркальном отражении φ→2π–φ. Это оправдывает сделанную нами замену 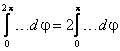
Скорость изменения r выразим через производную dφ/dt: 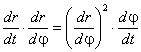 , ,
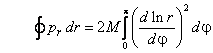 . .
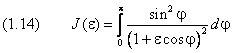 . .
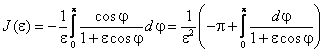 . .
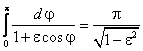 , ,
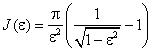 . .
Ещё одно алгебраическое уравнение вытекает из условия
постоянства полной энергии E. Чтобы вычислить кинетическую энергию, в
(1.6) заменим  . .
В формулу для потенциальной энергии (13.3.3) подставим r>из уравнения эллипса (1.5): Сложив (1.15) и (1.16), получим выражение для E:  . .
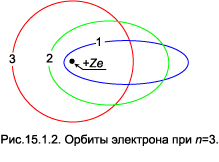
Подставив (1.18) в (1.17), получим окончательное выражение для E: Таким образом, полная энергия, как и в случае классического движения, зависит только от большой полуоси. Правило квантования для большой полуоси вытекает из (13.1.1), (1.10) и (1.18). Сопоставляя (1.20) с (13.5.1), видим, что большие полуоси эллипсов совпадают с радиусами соответствующих круговых орбит, а вместо единственного при круговом движении квантового числа nстоит сумма азимутального и радиального квантовых чисел — главное квантовое число. Малая полуось b зависит от обоих квантовых чисел в отдельности. В самом деле, принимая во внимание, что то есть, ту же самую формулу (13.5.2), что и для энергии стационарных круговых орбит. Но вместо числа, связанного с орбитальным моментом, стоит главное квантовое число. Подчеркнём, что их смысл различается коренным образом, несмотря на то, что они обозначаются одной и той же буквой n. Основное различие заключается в том, что главное квантовое число в теории Бора–Зоммерфельда не связано однозначно с моментом вращения: формула (13.3.7) для него лишена смысла. Эллиптические орбиты не меняют значений энергии стационарных состояний. Вместе с тем остаются в силе и все полученные из анализа круговых орбит выводы, касающиеся спектра водорода и сходных с ним ионов. Только каждому возможному значению энергии E соответствует не одна, а несколько орбит, различающихся эксцентриситетом. В случае круговых орбит энергия и момент определяются одним и тем же квантовым числом. При движении по эллипсу момент зависит от nφ, а энергия — от n, и между ними нет однозначной связи. Таким образом, представление об эллиптических орбитах позволяет объяснить явление вырождения энергетических уровней в атоме. Нулевому значению азимутального квантового числа соответствует прямая линия, проходящая через ядро. В классической механике движение по такой траектории невозможно, поэтому мы приходим к выводу, что nφ принимает только положительные значения. Отсюда в силу (1.11) приходим к выводу, что при фиксированной величине квантового числа n азимутальное и радиальное квантовые числа могут принимать следующие ряды значений: Итак, при заданной энергии E возможны n орбит разной формы. Чисто круговое движение имеет место, если nφ принимает максимально возможное значение, равное n, а наиболее вытянутый эллипс получается при nφ= 1. На рис.15.1.2 представлены три орбиты, соответствующие n=3. Цифрами указаны значения азимутального квантового числа nφ.
Итак, энергия атома
водорода в рассматриваемом приближении не зависит от орбитального момента.
Полученный результат не распространяется на все остальные атомы, но справедлив
только при движении в чисто кулоновском поле. Чтобы подчеркнуть это
обстоятельство, в литературе принято говорить о кулоновском, или случайном
вырождении. Особая роль кулоновского поля, как мы убедимся в следующей
главе, проявляется и в квантовой механике, где энергия атома также не зависит
от момента. Кулоновское вырождение (в нерелятивистском приближении) выделяет
атом водорода и водородоподобные ионы среди всех других атомных систем. С физической
точки зрения это объясняется более высокой симметрией движения в поле, где
потенциал падает обратно пропорционально расстоянию от центра, по сравнению с
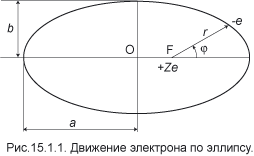
общим случаем центрально–симметричного поля. Но существует вырождение, которое имеет место у всех атомов, — вырождение по проекции момента на произвольную ось. В самом деле, если атом не помещён во внешнее поле, то его энергия не должна зависеть от ориентации в пространстве и, следовательно, от проекции любого вектора, в том числе, вектора орбитального момента. В полуклассической теории Зоммерфельда вырождение по проекции момента объясняется в рамках модели пространственного квантования. 15.2.Пространственное квантованиеПод влиянием внешнего поля — магнитного или электрического, — орбита электрона перестаёт быть плоской. Движение электрона становится трёхмерным и стационарные орбиты должны удовлетворять уже не двум, а трём квантовым условиям. Для удобства сопоставления с формулами первой главы, описывающими магнитные свойства атомов, в этом разделе считаем ядро бесконечно тяжёлым и, таким образом, не делаем различия между массой электрона me и приведённой массой m. Рассмотрим случай, когда внешнее поле можно считать малым по сравнению с полем ядра, а следовательно, невелико и изменение орбиты. Тогда орбита представляет собой прежний эллипс, а положение плоскости эллипса в пространстве определяется величиной и направлением внешнего поля. На рис. 15.2.1 введём сферические координаты r, θ, φ. 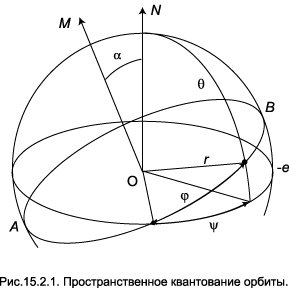
Пусть ON — направление внешнего поля; OM — нормаль к электронной орбите AB, составляющая угол a с прямой ON. Кроме того, введём азимут j, отсчитанный в плоскости орбиты. Полагая возмущение слабым, согласно сделанному предположению, будем считать справедливым правило квантования момента (1.7), выведенное нами для плоской орбиты. С другой стороны, в сферических координатах должны выполняться квантовые условия: (2.2) pψ = M cosα. Как и момент, его проекция
сохраняется во время движения, поэтому последнее из правил квантования (2.1)
даёт: Сравнивая (1.7), (2.2) и (2.3), находим: Таким образом, момент вращения может располагаться ровно 2nφ+1 различными способами по отношению к некоторому выделенному направлению, например, к вектору индукции магнитного поля. При отсутствии внешнего поля состояние с известной величиной момента является вырожденным с весом 2nφ+1. Полученный результат не зависит от формы потенциала и, в отличие от кулоновского вырождения, имеет место у каждого изолированного атома. Сравним формулу (2.5), полученную полуклассическим путём,
с результатом (12.3.5b)
квантовой теории. Легко убедиться, что первая получается из второй простой
заменой nφ на l и nψ на магнитное квантовое
число m. В этом пункте результаты классического и квантового
подходов почти совпадают. Различие заключается в следующем: классическая теория
описывает малые возмущения плоской
орбиты, а в квантовой механике связь (13.3.5) орбитального момента с его
проекцией справедлива всегда. 15.3. Эффект Зеемана.
Снятие вырождения по проекции момента приводит к эффекту Зеемана — расщеплению спектральных линий во внешнем магнитном поле. Из (1.3.3), (2.4) и (2.7) следует правило квантования потенциальной энергии при взаимодействии атома с магнитным полем: Изложим классический аспект эффекта Зеемана. Для этого сначала покажем, что внешнее магнитное поле вызывает ларморовскую прецессию — вращение электронной орбиты вокруг направления поля с постоянной угловой скоростью 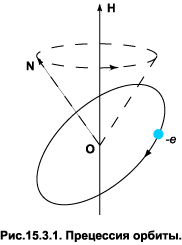
то есть сила Кориолиса уравновешивает силу Лоренца. Сделанное выше предположение о малости ΩH позволяет пренебречь центробежной силой, пропорциональной квадрату малой величины. Итак, во вращающейся системе координат орбита электрона останется прежним эллипсом, а относительно неподвижной — эллипсом, прецессирующим с частотой ΩH. Разделив энергию взаимодействия (3.1) на постоянную Планка, приходим к выводу, что спектральная линия в магнитном поле расщепляется на несколько компонент. Смещение частот между компонентами Dw равно целому числу WH. Для ∆m = 1 величина ∆ω равна Смещение линий в оптическом диапазоне принято выражать в шкале длин волн. Из формулы (3.3) с учётом λ = c/ν следует: Количество наблюдаемых компонент определяется весом нижнего и верхнего уровней перехода, а также правилом отбора. Самыми яркими являются переходы, удовлетворяющие правилам отбора для дипольного излучения. Сведения о них приведены в табл.15.3.1: Таблица 15.3.1. Правила отбора для магнитного квантового числа.
Такие переходы называются «разрешёнными». Интенсивность компонент с другими комбинациями магнитных чисел значительно ниже — на несколько порядков величины. На рис.(15.3.2) приведён случай, когда азимутальное квантовое число нижнего уровня равно двум, а верхнего — трём. При наблюдении в направлении, перпендикулярном к магнитному полю (случай а), круговые колебания проектируются в виде линейных, так что спектральная линия расщепляется на три линейно поляризованных составляющих — среднюю, с электрическим вектором волны вдоль поля, и крайние, с колебаниями поперёк поля. При наблюдении вдоль поля ( случай б) средняя составляющая пропадает, а две оставшиеся поляризованы по кругу: смещённая в красную сторону спектра — против часовой стрелки и смещённая в фиолетовую — по часовой стрелке. 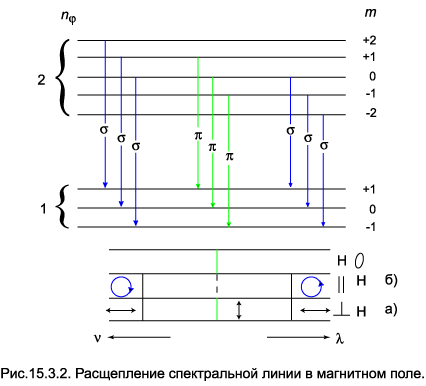
r¨ + ω02 ∙r, 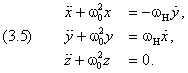
Отрицательный корень отвечает вращению по часовой стрелке. Этому направлению отвечает другая комплексная переменная: Если wH значительно меньше собственной частоты осциллятора, то Расщепление линий в магнитном поле было предсказано Лоренцом задолго до появления квантовой теории и экспериментально проверено Зееманом. Схема опыта Зеемана приведена на рис.15.3.3. 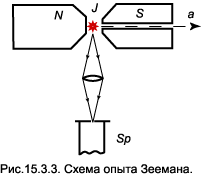
|
|||||||||||||||||||||||||||||||
| Вернуться к оглавлению |
| Перейти к следующей главе |