Вернуться к оглавлению
Вернуться к предыдущей главе Перейти к следующей главе


ГЛАВА 2.    ПУЛЬСИРУЮЩИЕ ЗВЕЗДЫ
 
2.1.   Общие сведения

         В 1878-1883 гг. немецкий физик А.Риттер впервые попытался объяснить звездную переменность пульсациями газовых шаров. Интересно, что русский астроном А.А.Белопольский (1854-1934), обнаруживший переменность лучевой скорости звезды d Цефея, в своей докторской диссертации 1896г. считал эту звезду, ныне общепризнанный прототип пульсирующих переменных, затменной. На защите ему возражал физик Н.А.Умов (1846-1915), догадавшийся об истинной причине изменений блеска звезды. В библиотеке ГАИШ хранится экземпляр диссертации Белопольского (изданной, как тогда полагалось, в виде брошюры) со злыми, скептическими пометками на полях, сделанными, кажется, В.К.Цераским. В 1899г. К.Шварцшильд обнаружил, что у звезд, подобных d Цефея, амплитуды изменения блеска в фотографических лучах намного превосходят амплитуды в визуальных лучах, и объяснил эффект изменениями температуры в результате пульсаций. (Вообще говоря, различие амплитуд возможно и у затменных переменных, если затмеваемый и затмевающий компоненты сильно различаются по спектральному классу, но в целом для затменных переменных значительные различия визуальной и фотографической амплитуды не очень характерны.)

         В 1918-1926гг. был опубликован цикл работ английского теоретика А.Эддингтона (1882-1944), посвященный исследованию адиабатических собственных радиальных колебаний газовых шаров. Эддингтон показал, что свободные колебания звезд должны быстро затухать, поэтому для звездных пульсаций необходимо наличие механизма, осуществляющего преобразование тепловой энергии в механическую энергию пульсаций. Таким образом, пульсирующая звезда представляет собой термодинамическую тепловую машину.

         В предположении малых колебаний Эддингтон вывел формулу для величины диссипации механической энергии колебаний W, возникающей при работе термодинамической тепловой машины:

(2.1)

Здесь dT/T есть относительное изменение температуры, возникающее в момент t в элементе массы "рабочего тела" dM, а dQ - количество тепла, поступающее за время dt в этот элемент массы. Первый интеграл берется по всем элементам "рабочего тела", а циклический интеграл - по циклу колебаний, т.е. по времени. Если W>0, механические колебания затухают, а если W<0 ("отрицательная диссипация") - раскачиваются. Случай "отрицательной диссипации" реализуется, если в некоторых зонах звезды поступление тепла dQ>0 происходит преимущественно в те моменты, когда температура среды повышается (например, из-за сжатия), то есть dT/T>0, и этот эффект полностью компенсирует положительную диссипацию, накапливаемую в остальных зонах.

         Эддингтон наметил и конкретные возможности реализации отрицательной диссипации в звездах. Так, отрицательная диссипация должна накапливаться в той зоне, где вырабатывается звездная энергия, в правдоподобном предположении, что источники звездной энергии эффективнее "работают" при более высоких температурах. Действительно, в этом случае при повышении температуры в зону будет поступать больше энергии. Окончательная идентификация термоядерной природы источников звездной энергии произошла уже после описываемых работ Эддингтона; при этом подтвердилась зависимость эффективности термоядерных источников энергии от температуры, и даже весьма сильная, причем в нужном для возникновения отрицательной диссипации смысле. Тем не менее сейчас считают, что механизм пульсаций, основанный на зоне источников энергии звезды, в большинстве случаев неэффективен. Дело в том, что расчеты моделей пульсирующих звезд приводят к выводу о быстром спаде относительной амплитуды пульсаций по мере продвижения от периферии звезды к ее центру; роль центральной зоны в пульсациях оказывается малой, а большая положительная диссипация, накапливаемая в поверхностных зонах, остается нескомпенсированной.

         Второй механизм, предложенный Эддингтоном, сам он считал "фантастическим для тепловой машины, но не обязательно фантастическим для звезды". Действие этого механизма можно уподобить конструкции двигателя, в котором вместо того, чтобы организовать поступление тепла в момент сжатия, предусмотрели уменьшение оттока энергии из цилиндра при сжатии. В случае звезды это означает ситуацию, в которой непрозрачность увеличивается при сжатии. Такой механизм часто называют клапанным, поскольку некий физический процесс должен играть роль клапана, регулирующего отток тепла. Эддингтон не отождествил механизм-клапан и вообще считал свой второй механизм резервом на крайний случай, если ничего более правдоподобного предложить не удастся. Другое распространенное название второго механизма Эддингтона - каппа-механизм, поскольку непрозрачность звездного вещества в астрофизике обычно обозначают греческой буквой k (каппа).

         В 1950-е годы С.А.Жевакин (1916-2001), советский физик из г.Горького (Н.Новгород), открыл тот конкретный вариант k -механизма, который ответственен за пульсации переменных звезд многих типов, в частности, цефеид, переменных типа RR Лиры и многих других. Основную роль в механизме Жевакина играет так называемая зона двукратной критической ионизации гелия. Это та зона, в которой в течение цикла пульсаций гелий то ионизуется до "голого" ядра, то вновь рекомбинирует до однократно ионизованного состояния. При сжатии температура повышается, гелий ионизуется, на это уходит энергия, которая, таким образом, задерживается в рассматриваемой зоне. При последующем расширении гелий рекомбинирует, энергия высвечивается и уходит из зоны наружу. Мы видим, что этот процесс вполне соответствует идее Эддингтона. Жевакин довел свою теорию до расчетов простейших пульсационных моделей, даже не прибегая к электронным вычислительным машинам. Впоследствии американский астрофизик Р.Кристи, используя крупнейшие компьютеры 60-х годов (сегодня представляющиеся примитивными), показал, что, вопреки первоначальному мнению Жевакина, немаловажную роль играет и зона критической ионизации водорода. На рис. 2.1 схематически показано расположение зон критической ионизации внутри звезды. Видно, что эти зоны весьма близки к поверхности.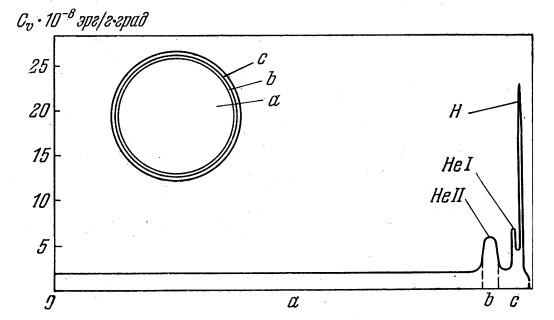

Рис. 2.1.  Схема расположения зоны отрицательной диссипации внутри звезды (по С.А.Жевакину): (a) - внутренняя область звезды, (b) - зона отрицательной диссипации, (c) - атмосфера звезды. Внизу представлено изменение удельной теплоемкости при постоянном объеме cv и расположение зон критической ионизации He II, He I и H внутри звезды.

         В задачи нашего курса не входит детальное рассмотрение физики звездных пульсаций; мы ограничимся качественным рассмотрением некоторых важнейших следствий из соответствующей теории. Интересующихся отсылаем к читающемуся на астрономическом отделении спецкурсу Ю.А.Фадеева "Теория звездных пульсаций". В Приложении приведена сводка основных уравнений, лежащих в основе пульсационных расчетов.

         Система уравнений звездных пульсаций является нелинейной, что усложняет ее решение. В случае малых колебаний уравнения можно линеаризовать. Линейная пульсационная теория позволяет найти области диаграммы Герцшпрунга-Рессела, в которых звезда окажется неустойчивой в тех или иных пульсационных модах, а также определить периоды всех мод пульсаций каждой звездной модели. Однако она не в состоянии предсказать форму кривой блеска при пульсациях с полной амплитудой, а также, в случае неустойчивости сразу в нескольких модах, определить характер установившихся пульсаций.

         Говоря о пульсациях звезд, мы пока имеем в виду радиальные пульсации, при которых частицы в звездной атмосфере движутся вверх и вниз, по вертикали. При этом основной модой называют такое колебание, при котором на поверхности звезды находится пучность стоячей волны, в центре - узел, а в промежутке других узлов нет. Если между поверхностью звезды и ее центром есть еще один узел, говорят, что звезда пульсирует в первом обертоне (первой гармонике); два промежуточных узла соответствуют второму обертону, и т.д. Поверхность звезды всегда соответствует одной из пучностей. О нерадиальных пульсациях звезд будет говориться в последующих лекциях.

         Звезды, пульсации которых объясняются классическим механизмом Жевакина, на диаграмме Герцшпрунга-Рессела занимают обширную область (полосу) нестабильности, наискось пересекающую диаграмму сверху вниз (рис. 2.2). Поскольку в рассматриваемую область попадают цефеиды, ее часто называют цефеидной полосой нестабильности. Кроме цефеид, в ней можно найти переменные звезды нескольких других типов. Основные типы переменных звезд в цефеидной полосе, в порядке уменьшения средней светимости, таковы: звезды типа RV Тельца; классические цефеиды; цефеиды сферической составляющей (звезды типа W Девы); переменные типа RR Лиры; звезды типа d Щита и SX Феникса; переменные типа ZZ Кита. Названные типы охватывают все классы светимости, от сверхгигантов до белых карликов. Есть пульсирующие переменные даже среди звезд главной последовательности (Жевакин считал, что компактная структура этих звезд исключает пульсации) - здесь находится большая часть звезд типа d Щита.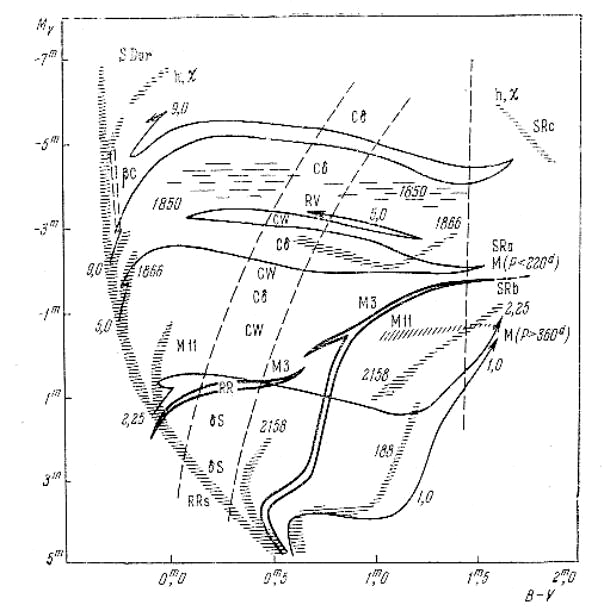

Рис. 2.2.  Пульсирующие звезды на диаграмме Герцшпрунга-Рессела. Обозначения типов соответствуют номенклатуре 3-го издания ОКПЗ.

         Несколько других типов пульсирующих переменных звезд расположены на диаграмме Герцшпрунга - Рессела вне цефеидной полосы нестабильности. В последние десятилетия их переменность также находит объяснения в рамках несколько модифицированного k-механизма. Сравнительно недавно радикальному пересмотру подверглись наши представления о коэффициенте непрозрачности в звездных недрах. В результате использования новых непрозрачностей в пульсационных расчетах было установлено, что области нестабильности охватывают весьма обширные регионы на диаграмме Герцшпрунга - Рессела, а зоны относительной стабильности являются скорее исключением. Эти выводы подтверждаются результатами космического эксперимента HIPPARCOS, в сущности, не нашедшего областей диаграммы Герцшпрунга - Рессела, полностью свободных от проявлений пульсационной неустойчивости.

         Кратко остановимся на возможности оценки эволюционных изменений периода переменной звезды. Еще Эддингтоном было показано (для случая свободных адиабатических колебаний), что между периодом и средней плотностью звезды должно существовать соотношение

(2.2)

где Q - так называемая пульсационная постоянная. Применимость этого соотношения не ограничивается свободными адиабатическими колебаниями газовых шаров, но в случае реальных звезд величину Q нельзя считать постоянной в строгом смысле слова, она несколько зависит от структуры звезды. Тем не менее, эта величина практически одинакова для переменных звезд одного типа, не слишком различающихся своими периодами, и тем более для одной звезды в два близких момента времени. В формуле Эддингтона легко усмотреть достаточно глубокие аналогии с аналогичными соотношениями, скажем, для колебаний математического или пружинного маятника; в последней аналогии средняя плотность как бы играет роль жесткости пружины. Предположим, что звезда эволюционирует, меняя светимость, радиус, эффективную температуру. Тогда, учитывая, что 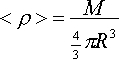  ,   а 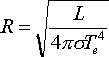     нетрудно получить:


(2.3)

Величины в правой части формулы (2.3) можно оценить из эволюционных расчетов для подходящих звездных моделей и, таким образом, вычислить ожидаемые изменения периода и сравнить их с наблюдаемыми. Более точная, но при этом и намного более громоздкая (при не очень значительном повышении точности) методика оценки заключается в расчете конкретных пульсационных моделей для последовательных стадий эволюции.

         Знаки членов в правой части уравнения (2.3) вполне понятны из физических соображений. Если у звезды возрастает светимость при неизменной эффективной температуре, значит, возрастает излучающая поверхность, то есть растет радиус звезды. При этом убывает средняя плотность звезды; в аналогии с маятником это эквивалентно уменьшению жесткости пружины или ускорения силы тяжести. Значит, период будет возрастать. Аналогично, в случае уменьшения эффективной температуры при постоянной светимости тот факт, что светимость не меняется, означает, что радиус звезды увеличивается.

         Наблюдая пульсирующую переменную звезду на протяжении большого количества циклов, мы можем выявить даже небольшие изменения ее периода. Таким образом, появляется уникальная возможность непосредственно в наблюдениях выявить эффекты звездной эволюции. О результатах практического применения подобного подхода будет сказано в следующих лекциях.

Вернуться к оглавлению
Вернуться к предыдущей главе Перейти к следующей главе