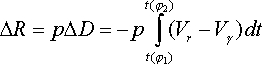| Вернуться к оглавлению |
| Перейти к следующей главе |
|
||
|
|
Обратимся теперь к отдельным типам пульсирующих звезд. И, конечно, мы начнем с цефеид - не
потому, что это самый богатый звездами тип (это не так), а ввиду огромной роли цефеид в астрономии.
Прежде к цефеидам относили без разбору все звезды, сходные с настоящими цефеидами по морфологии кривой блеска, то есть два современных главных подтипа (классические цефеиды, DCEP и DCEPS в обозначениях ОКПЗ, и цефеиды сферической составляющей, CWA и CWB) и "короткопериодические цефеиды", то есть все разновидности переменных типа RR Лиры. Мы сейчас будем рассматривать классические цефеиды, то есть долгопериодические цефеиды, относящиеся к плоской составляющей Галактики. Многочисленными исследованиями были установлены закономерности, связывающие форму кривой блеска цефеид с продолжительностью периода (последовательность Герцшпрунга, см. ниже). Ряд звезд в эту последовательность не укладывается; их кривые блеска сходны с кривыми блеска цефеид в шаровых скоплениях. В 1949г., принимая во внимание особенности пространственного распределения (большие z-координаты) "аномальных" цефеид (интересно, что введенный Б.В.Кукаркиным термин "аномальная цефеида" позднее, когда "аномальные цефеиды" по Кукаркину все уже давно называли звездами типа W Девы, вновь ввели уже для звезд типа BL Волопаса. См. об этом в следующих лекциях) и их отличия от большинства цефеид по другим характеристикам, Б.В.Кукаркин высказал идею о различном происхождении этих звезд. Большинство цефеид (классические цефеиды) принадлежат к плоской составляющей Галактики, а "аномальные" цефеиды и цефеиды в шаровых скоплениях - к сферической. Периоды надежно классифицированных классических цефеид нашей Галактики заключены в пределах от 1d до 45d. Известно несколько звезд с более продолжительными периодами (до 125d), но их принадлежность к классическим цефеидам достоверно не установлена. Любопытно, что в других галактиках (прежде всего в Магеллановых Облаках) обнаружены звезды со всеми признаками цефеид (стабильность периода и формы кривой блеска, спектр, светимость) даже с периодами, превосходящими 200d. В 4-м издании ОКПЗ к классическим цефеидам отнесено 460 звезд, к цефеидам сферической составляющей - 173, а 180 звезд классифицированы просто как цефеиды, поскольку для них принадлежность к той или иной составляющей Галактики не была точно известна. На самом деле в этой группе классические цефеиды тоже, несомненно, преобладают. Тысячи цефеид выявлены в ближайших галактиках (прежде всего в Магеллановых Облаках и в галактике Андромеды M 31). Исключительно важным свойством цефеид, во многом определяющим значение этих звезд для астрономии, является существование зависимости период-светимость. Х.Ливитт в 1908г. открыла 1777 переменных звезд в Малом Магеллановом Облаке (ММО). Для 16 из них она определила периоды; оказалось, что чем продолжительнее период, тем ярче звезда. Разумеется, при огромном расстоянии до ММО по сравнению с размером самого облака этот факт следует интерпретировать как зависимость светимости (а не только видимой величины) от периода. Вполне понято, что открытые мисс Ливитт переменные звезды - это цефеиды, было не сразу. Впервые на это четко указал Э.Герцшпрунг в 1913г. Ему же принадлежит идея о неоценимой роли зависимости период-светимость для определения расстояний до отдельных цефеид, а также до звездных систем, их содержащих. Герцшпрунг установил нуль-пункт зависимости период-светимость, определив по собственным движениям 13 цефеид статистический параллакс. С уже известным нуль-пунктом он применил зависимость период-светимость для определения расстояния до ММО. В 1918г. Х.Шепли ревизовал зависимость период-светимость. Он использовал данные о цефеидах в Магеллановых Облаках, в шаровых скоплениях и в окрестностях Солнца. (Сегодня мы знаем, что выборка Шепли неоднородна, и не все эти звезды имеют одинаковую светимость при одинаковом периоде.) Полученный Шепли вариант зависимости период-светимость был в употреблении более 30 лет и привел к подлинной революции в астрономии. Была доказана внегалактическая природа спиральных туманностей, установлено положение Солнца в Галактике. К концу 1940-х годов стали накапливаться данные, требующие пересмотра зависимости Шепли. Рекомендую прочитать интересный рассказ об этом периоде в лекциях В.Бааде "Эволюция звезд и галактик", опубликованных в 1966г. на русском языке. Вкратце наиболее существенный аргумент в пользу пересмотра зависимости сводился к тому, что при принятой форме зависимости и наблюдаемых видимых величинах цефеид в галактике M 31 в ней должны были, при достигнутых предельных величинах при фотографировании на 5-м телескопе, наблюдаться и звезды типа RR Лиры, но они оставались недоступными для наблюдений. (В ту пору для всех звезд типа RR Лиры принимали абсолютную фотографическую величину 0m.0, так что для определения модуля расстояния этих звезд оказывалась ненужной даже единственная операция вычитания.) Был сделан вывод о необходимости придания к нуль-пункту зависимости Шепли для цефеид поправки в -1m.5 (это значит, что при данном периоде мы считаем цефеиды более яркими) или придания к абсолютным величинам звезд типа RR Лиры поправки в +1m.5. Поправка порядка 1m очень существенна. Цефеиды - основное орудие в деле установления шкалы расстояний во Вселенной. Именно цефеиды, достаточно яркие звезды для фотометрического изучения в галактиках, уже настолько удаленных, чтобы красное смещение за счет расширения Вселенной превзошло пекулярные скорости, используются для определения постоянной Хаббла, для калибровки других критериев расстояния. Очевидно, ошибка в светимости цефеид в 1m ведет к ошибке в расстояниях в В качестве примера приведем современный вариант зависимости период-светимость, выведенный Л.Н.Бердниковым и др. в 1996г.
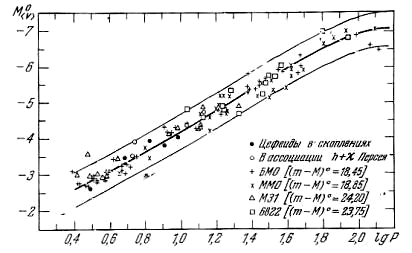
Вариант зависимости период-светимость, представленный на графике (рис. 2.3), предложили в 1968г. А.Сэндидж и Г.Тамманн. Из рисунка видно, что дисперсия зависимости не очень мала. Важный вопрос - является ли эта дисперсия реальной или она связана с ошибками наблюдений. Этот вопрос еще в 1958г. Сэндидж исследовал теоретически. Он исходил из того, что зависимость период-светимость была бы "ниточной", если бы полоса нестабильности на диаграмме Герцшпрунга-Рессела была бесконечно узкой по цветовой координате. Так как полоса нестабильности не перпендикулярна оси абсцисс на диаграмме Герцшпрунга-Рессела, а наклонна, должна существовать зависимость период-цвет. А поскольку полоса нестабильности имеет конечную ширину, дисперсия обеих зависимостей, период-светимость и период-цвет, должна быть реальной. Представление о достаточно простых выкладках, иллюстрирующих рассуждения Сэндиджа и основанных на приведенной выше формуле (2.2), можно найти в книге "Пульсирующие звезды" из пятитомной серии монографий (стр. 82); там же приведены ссылки на работы, где выкладки воспроизведены в более полном виде. Попытки вывести зависимость период-светимость-цвет из наблюдений предпринимали многие исследователи. Выяснилось, однако, что коэффициент при показателе цвета в этой зависимости определяется ненадежно и плохо воспроизводится от одного исследования к другому. Хотя никто не отрицает справедливости рассуждений Сэндиджа, на практике для определения расстояний во Вселенной предпочитают пользоваться традиционной зависимостью период-светимость, без цветового члена. Зависимость период-светимость позволяет установить положение цефеиды в пространстве. Классические цефеиды отличаются высокой степенью концентрации к плоскости Млечного Пути. Среднее абсолютное значение Z-координаты цефеид составляет около 65 пк. В конце 1940-х гг. именно изучение распределения цефеид по Z-координате дало Б.В.Кукаркину важный аргумент в пользу необходимости выделения цефеид сферической составляющей в отдельный тип. Он нашел, что звезды с Z-координатой, превышающей по модулю 1000 пк, должны были бы, при известной концентрации цефеид к галактической плоскости, встречаться не чаще чем одна на 20000, однако таких звезд было известно более 50 - одна из девяти. Тогда же Кукаркин пришел к выводу, что цефеиды плоской составляющей обладают более высокой светимостью. Что касается распределения цефеид в плоскости Галактики, то связь со спиральными ветвями более четко выявляется для цефеид с большими периодами. Цефеиды со сходными характеристиками (скажем, близкими периодами; как мы увидим далее, это говорит о близком возрасте) образуют в пространстве группировки размерами 200-1000 пк, обрисовывая выделенные Ю.Н.Ефремовым звездные комплексы, являющиеся, по-видимому, массивными группами звезд совместного происхождения. С проблемой пространственного распределения связан вопрос о членстве цефеид в звездных скоплениях. В шаровых скоплениях встречаются цефеиды, но это цефеиды сферической составляющей, о них мы будем говорить в последующих лекциях. Еще в середине 20-го века было распространено мнение, что в рассеянных скоплениях переменные звезды не встречаются вообще (П.Н.Холопов вспоминал, как основоположники отечественной школы исследователей переменных звезд П.П.Паренаго и Б.В.Кукаркин относили заподозренные звезды к объектам "второго сорта", с номерами КЗП (см. главу 1), превышающими 100000, только из-за принадлежности к рассеянному скоплению - считалось, что там "настоящих" переменных звезд не бывает). Это мнение бытовало несмотря на то, что еще в 1920-е гг. П.Дойг указал, что цефеиды U Sgr и S Nor лежат в рассеянных скоплениях M 25 и NGC 6087, соответственно. Впервые вопрос о реальности физической связи цефеид со скоплениями исследовал П.Н.Холопов, опубликовавший в 1956г. список 16 цефеид, проецирующихся на скопления. Холопов использовал методику "сводного скопления", то есть как бы подменил все скопления одним, приведя размеры всех скоплений к одному масштабу. Далее он вычислил вероятность случайного попадания наблюдаемого числа переменных звезд разных типов в центральный круг сводного рассеянного скопления. Для цефеид эта вероятность оказалась равной 0.00171. Холопов обнаружил также увеличение концентрации цефеид по мере приближения к центру сводного скопления, что также следует рассматривать как доказательство реальности физической связи цефеид со скоплениями. В настоящее время известны десятки цефеид - членов рассеянных скоплений. Были и случаи, когда сначала обнаруживали цефеиду, а затем выявляли скопление вокруг нее. Цефеиды - члены скоплений нередко используют для калибровки зависимости период-светимость. Присутствие цефеид в рассеянных скоплениях облегчает понимание эволюционного статуса этих звезд. (Вообще, обращение к звездным скоплениям - довольно мощный прием выяснения эволюционного места входящих в скопления звезд.) Цефеиды - это звезды, уже прошедшие стадию главной последовательности (тогда они были B-звездами) и направившиеся после этого в область красных сверхгигантов. На рис. 2.4 показаны эволюционные треки. Видно, что звезды пересекают полосу нестабильности, как правило, не один раз. Первое пересечение занимает очень мало времени (~103 лет), и цефеид на стадии этого пересечения, среди наблюдаемых объектов, должно быть мало. Следующие пересечения занимают намного больше времени. 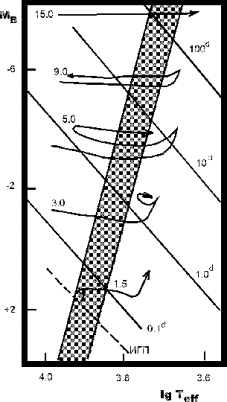
Из рисунка видно, что чем больше масса звезды, тем больший период имеет звезда в полосе нестабильности. Чем массивнее звезда, тем быстрее она уходит с главной последовательности и становится цефеидой. Следовательно, должна существовать зависимость между возрастом скопления (который можно определить по положению точки поворота главной последовательности на диаграмме Герцшпрунга-Рессела) и периодом входящих в него цефеид, означающая, в сущности, зависимость между периодом любой классической цефеиды (включая звезды поля) и ее возрастом. Такая зависимость действительно была обнаружена в середине 1960-х гг. Ю.Н.Ефремовым. Эту зависимость можно использовать для определения возраста классических цефеид, не входящих в скопления, для изучения особенностей кинематики в зависимости от возраста и т.п. Такая простая возможность определения возраста индивидуальной звезды представляется совершенно уникальной в современной астрофизике. Конкретная форма зависимости период-возраст зависит от металличности соответствующего звездного населения. Приведем для примера вариант зависимости период-возраст, предложенный Ц.Г.Цветковым (Болгария) в 1980г.
Эволюционная теория предсказывает, что при массах меньше 4 M¤ звезды пересекают полосу нестабильности только один раз, причем это прохождение - быстрое. Предсказание находится в согласии с наблюдаемым фактом, что при малых периодах число цефеид резко падает, хотя число B-звезд с уменьшением светимости растет. Классические цефеиды имеют характерные асимметричные кривые блеска с более быстрым подъемом и более медленным спадом. В качестве примера на рис. 2.5 показана кривая блеска звезды d Цефея, полученная в 1930-е гг. Н.Ф.Флорей при помощи визуального фотометра и демонстрирующая также высокую точность этого совершенно оставленного сейчас метода наблюдений. Амплитуда изменения блеска цефеид в синих (скажем, фотографических) лучах заметно больше, чем в визуальных (например, AV = 0.67 AB). На заре исследования цефеид это обстоятельство было правильно интерпретировано как проявление пульсаций: в максимуме блеска цефеиды имеют более высокую температуру, чем в минимуме. 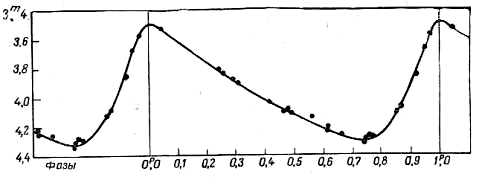
Л.Н. Бердников и его соавторы выполнили в последние годы огромный объем высокоточных фотометрических наблюдений цефеид (в основном фотоэлектрических) и собрали весьма полную компилятивную базу данных по фотометрии цефеид. Существование зависимости характерной формы кривой блеска цефеид от продолжительности периода, как уже отмечалось, впервые заметил Э.Герцшпрунг, эта зависимость так и называется последовательностью Герцшпрунга. Ее неоднократно исследовали разные авторы; отметим, в частности, исследование Б.В.Кукаркина и П.П.Паренаго 1937г. До периода в 6d кривые блеска обычно имеют гладкую форму, как мы видели для d Цефея (P=5d.37). При P~6d на нисходящей ветви зарождается горб (U Стрельца: P=6d.74 см. рис. 2.6). При дальнейшем увеличении периода горб растет и приближается к максимуму. Близ периода в 9-10 суток горб весьма велик, кривая блеска имеет иногда два почти одинаковых максимума. При еще больших периодах горб переходит на восходящую ветвь и постепенно ослабевает. Сейчас эту последовательность чаще всего связывают с соизмеримостью периодов основного тона и второго обертона при периодах основного тона около 9-10 суток, в результате чего на кривой блеска проявляются резонансные явления. 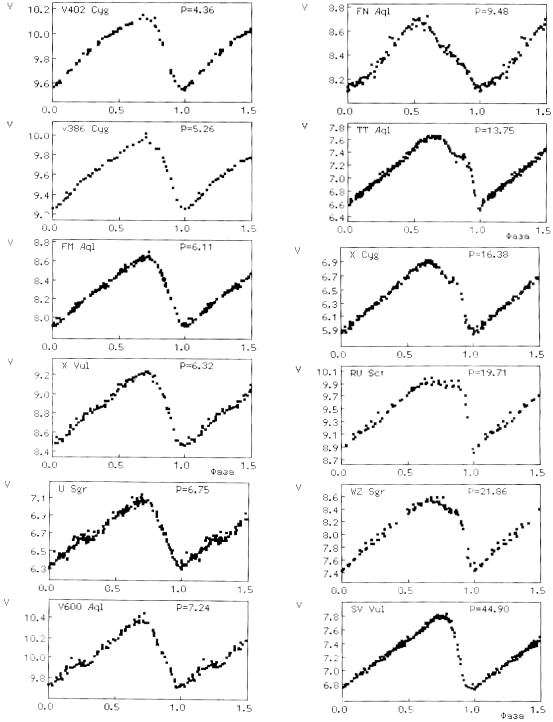
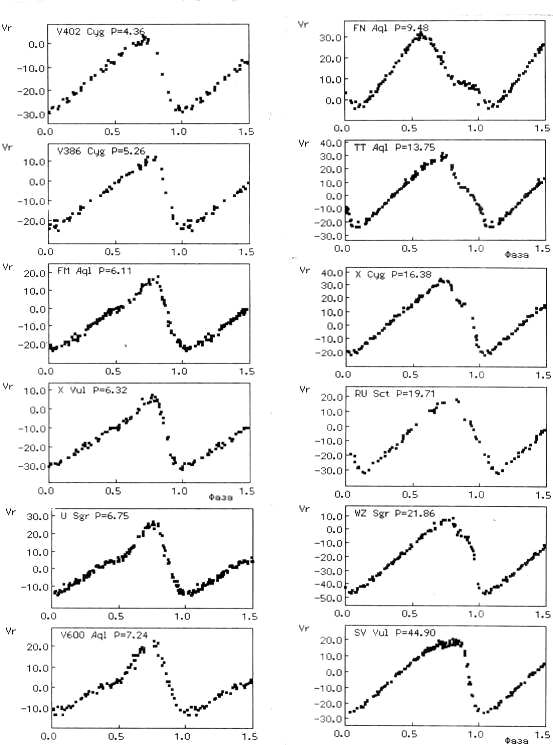
Среди классических цефеид (тип DCEP по классификации ОКПЗ) выделяется подтип DCEPS, характеризующийся синусоидальными кривыми блеска и пониженными амплитудами переменности. Распространено, хотя окончательно и не доказано, объяснение таких звезд как пульсаторов в первом обертоне. Одно время считалось, что такие звезды преобладают при периодах в 9-10 суток, где у звезд, укладывающихся в последовательность Герцшпрунга, наблюдается переход горба на кривой блеска с одной ветви на другую. Сейчас синусоидальные цефеиды специально не связывают с указанным интервалом периодов, хотя следует признать, что на переходных периодах многие зависимости для цефеид терпят излом. Даже зависимость период-светимость иногда представляют различными формулами для периодов до 10 и свыше 10 суток. Интерпретации цефеид типа DCEPS в нашей Галактике мешает то обстоятельство, что критерии, которые позволяли бы установить моду пульсации цефеиды по наблюдательным данным, до последнего времени не были разработаны. В то же время моду пульсации сравнительно легко определить, например, для цефеид Магеллановых Облаков. В каждой из этих двух галактик цефеиды находятся практически на одинаковом расстоянии от земного наблюдателя. Зависимость период-светимость для цефеид, скажем, БМО, пульсирующих в основном тоне, будет отличаться от аналогичной зависимости для цефеид той же галактики, пульсирующих в первом обертоне: при той же светимости период "обертонной" цефеиды будет более коротким. Большое количество цефеид в Магеллановых Облаках было открыто в 1990-е годы в качестве побочного результата проекта поиска гравитационного микролинзирования OGLE. На рис. 2.8 показана зависимость среднего блеска этих цефеид (в БМО) от логарифма периода. Левую последовательность составляют цефеиды, пульсирующие в первом обертоне. 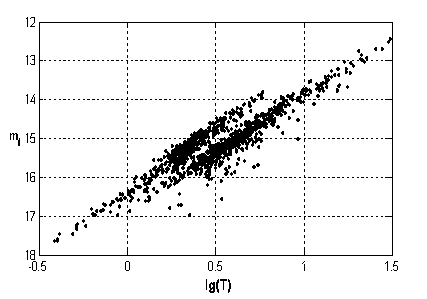
В защищенной в 2001/2002 году на Астрономическом отделении МГУ дипломной работе И.Егорова на основе параметров кривых блеска цефеид нашей Галактики, которые были сопоставлены с аналогичными параметрами кривых блеска цефеид Магеллановых Облаков, использованных в качестве обучающей выборки, определена мода пульсаций цефеид нашей Галактики из ОКПЗ. Более 3/4 звезд типа DCEPS оказались пульсирующими в первом обертоне, что в целом подтверждает существовавшие ранее представления. В интервале периодов от 2 до 4 суток встречается немалый процент цефеид с двойной периодичностью, то есть звезд, показывающих биения двух колебаний. В ОКПЗ такие звезды отнесены к типу CEP(B). В нашей Галактике из полутора десятков цефеид типа CEP(B) только одна пульсирует в первом обертоне и во втором обертоне, а все остальные - в основном тоне и в первом обертоне (моды пульсаций отождествляют, сравнивая наблюдаемое отношение двух периодов с предсказаниями пульсационной теории). В Магеллановых Облаках звезды, пульсирующие в первом и втором обертонах, более многочисленны (в Галактике известны две звезды, AC Андромеды и V823 Кассиопеи, пульсирующие одновременно в трех модах - основном тоне, первом и втором обертонах. Это довольно короткопериодические звезды, и не до конца ясно, следует ли рассматривать их вместе с цефеидами или вместе с переменными типа RR Лиры). Исследование таких звезд дает интересную возможность определения их масс и радиусов. Линейная теория пульсаций связывает периоды основного тона (P0) и первого обертона (P1) определенными соотношениями с массой и радиусом: P0= f0 (R,M), P1= f1 (R,M). Это дает систему из двух уравнений для определения двух неизвестных, массы и радиуса.На протяжении ряда лет в связи с этим была известна проблема расхождения "эволюционных" и "пульсационных" масс: такой метод давал для цефеид массы порядка одной солнечной. После упоминавшегося выше уточнения звездных непрозрачностей проблема была снята, а "эволюционные" массы (порядка 5 солнечных для цефеид с биениями) признаны верными. Следует, однако, иметь в виду, что если линейная теория пульсаций, по-видимому, предсказывает для звезд типа CEP(B) правильные значения периодов, нелинейная теория пульсаций испытывает затруднения в объяснении причины достаточно устойчивого сосуществования пульсаций двух видов для одной звезды. Спектры цефеид в минимуме блеска мало отличаются от спектров нормальных сверхгигантов; класс светимости с увеличением периода изменяется от II до Ia, а спектральный класс становится все более поздним, от F7 до K1. В максимуме блеска спектральные классы цефеид почти не зависят от периода и заключены между F5 и F8. У цефеид с периодами, превышающими 4d, вскоре после минимума блеска наблюдается эмиссия в линиях Ca II. С ростом периода она занимает все большую долю цикла, не превышающую, однако, 0.4 периода. Важный источник информации о цефеидах - кривые лучевых скоростей. Приведенные к Солнцу скорости представляют, подобно кривой блеска, в зависимости от фазы пульсационного цикла. В случае высокоточных измерений лучевых скоростей, например, полученных по программе ГАИШ и ИНАСАН с корреляционным спектрометром ИЛС конструкции А.А.Токовинина, кривые лучевых скоростей многих звезд характеризуются малым разбросом точек, что говорит о хорошей воспроизводимости пульсационных процессов от цикла к циклу и о стабильности периода (см. рис. 2.9). В конце 1990-х годов Н.А.Горыня выявила в кривых лучевых скоростей классических цефеид закономерность, аналогичную последовательности Герцшпрунга для кривых блеска (рис. 2.7). Следует отметить, что изменения блеска - сложный процесс, вызванный изменениями как размера звезды, так и температуры ее поверхности, в то время как изменения лучевой скорости прямо связаны с изменениями линейных размеров, поэтому интерпретация последовательности форм кривых лучевых скоростей в зависимости от периода более привлекательна для теоретиков, чем интерпретация классической последовательности Герцшпрунга. Фурье-анализ кривых лучевых скоростей является также эффективным инструментом идентификации моды пульсаций и выявления всевозможных резонансов. Такие работы в последние годы активно проводит П.Москалик (Варшава). 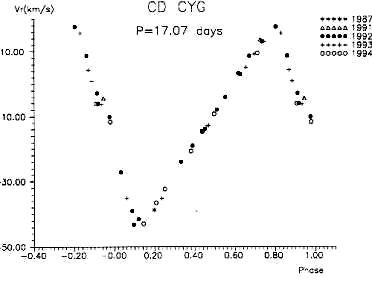
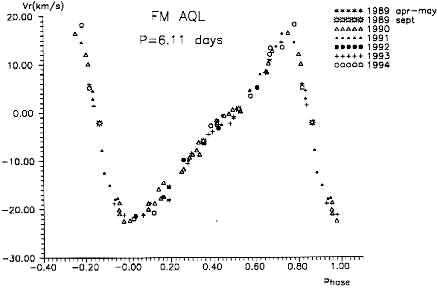
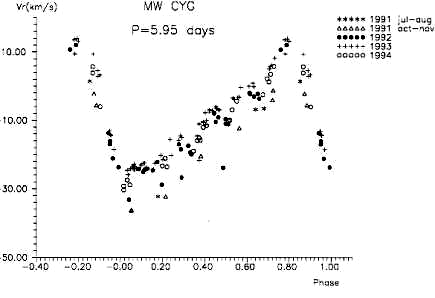
В литературе можно увидеть утверждения, что кривая лучевых скоростей является почти точным зеркальным отражением кривой блеска. Более точные современные измерения лучевых скоростей показали, что это не вполне так, но все же максимум блеска примерно совпадает с минимумом лучевой скорости (максимальной скорости расширения звезды). Заметно повышенный разброс точек наблюдается на кривых лучевых скоростей цефеид с биениями; наличие большого числа наблюдений позволяет разделить колебания лучевой скорости с двумя периодами. Еще одна возможная причина повышенного разброса точек на кривых лучевых скоростей, "свернутых" с орбитальным периодом - двойственность цефеид (рис. 2.10). Как правило, спектрально-двойные цефеиды, как сверхгиганты, характеризуются весьма большими орбитальными периодами (несколько лет), поэтому на кривой блеска появляется расслоение наблюдений на отдельные сезоны, как показано на рисунке. Три цефеиды, AU Peg, IX Cas и TX Del, показывают необычно короткие орбитальные периоды (от 2 до 4.5 месяцев); не исключено, однако, что эти объекты не принадлежат к классическим цефеидам. На особый случай этих звезд впервые четко указали в 1989г. Х.Харрис и Д.Уэлч. Собрав большое число наблюдений за несколько сезонов, удается разделить пульсационные и орбитальные движения, определить орбитальный период и другие элементы орбиты, оценить функцию масс системы. У цефеиды SU Cyg обнаружен массивный спутник слабого блеска; высказывались даже предположения о его релятивистской природе, но оказалось, что спутник, в свою очередь, является двойной системой. Результаты московской программы измерений лучевых скоростей цефеид говорят о том, что не менее четверти цефеид входят в двойные и кратные системы; намного более высокие оценки доли двойных среди цефеид, предлагавшиеся Л.Сабадошем (до 60%), не представляются нам, однако, достаточно обоснованными. 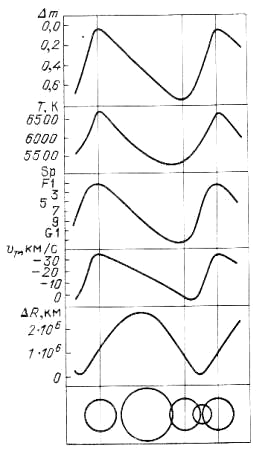
Если для радиально пульсирующей звезды получены достаточно точные наблюдения блеска в нескольких полосах и измерения лучевой скорости, то для определения ее радиуса можно применить остроумный способ, идею которого впервые высказал В.Бааде в 1920-е и развил А.Весселинк в 1940-е гг. Этот способ так и называется методом Бааде-Весселинка, предложены многочисленные его модификации, причем ниже описана не самая эффективная, но достаточно "прозрачная" с точки зрения физических оснований модификация метода. 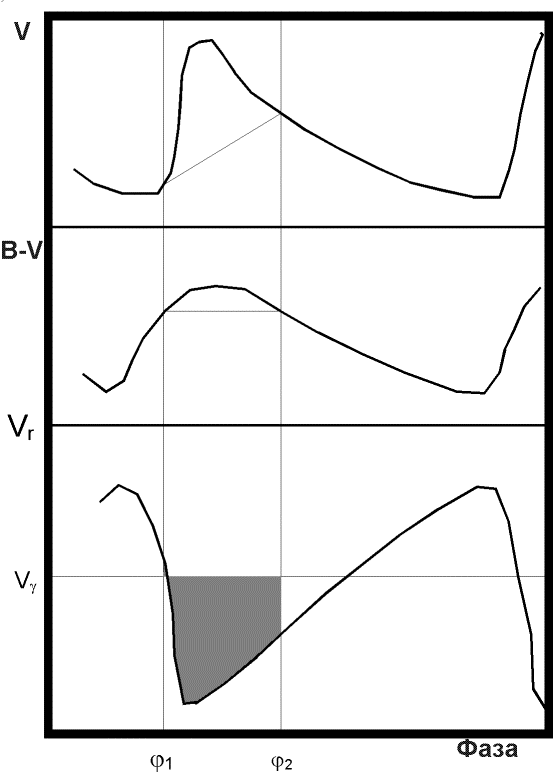
Пусть в нашем распоряжении имеются (рис. 2.12) кривая блеска, кривая показателя цвета и кривая лучевых скоростей. На рисунке использованы величина V и показатель цвета B-V; этот выбор, если позволяют наблюдения, может быть и другим, в частности, можно рекомендовать использование величин и показателей цвета в красном и ближнем инфракрасном диапазоне. Выберем две фазы, f1 и f2, такие, что (B-V)(f1)=(B-V)(f2). Будем пока считать, что показатель цвета определяется только температурой, так что из равенства показателей цвета следует, что T1=T2. Соответствующие этим двум фазам звездные величины, однако, не совпадают, поскольку изменился радиус звезды. Запишем в предположении малых колебаний (это предположение не является существенным ограничением общности, во многих модификациях метода переход к колебаниям, которые нельзя считать малыми, легко осуществляется при помощи итерационного процесса):
Величину DR нетрудно определить из кривой лучевых скоростей:
В формуле (2.5) Vg - средняя за период лучевая скорость. С этой скоростью движется по лучу зрения центр масс звезды. Нуждается в пояснении и множитель p. Если бы мы могли измерять лучевую скорость центра диска звезды, этот множитель был бы не нужен. Но мы измеряем лучевую скорость, усредненную по звездному диску. Края диска движутся из-за пульсаций в направлении, перпендикулярном к лучу зрения, и уменьшают наблюдаемые колебания скорости. В то же время вклад различных частей диска искажается наличием потемнения диска к краю. Очевидно, множитель p больше единицы. Для определения множителя p прибегают к теории звездных атмосфер. В первых вариантах метода Бааде-Весселинка принимали p=24/17. В современных работах используют значения p, равные 1.31 или 1.32. Выбрав несколько пар f1 и f1, характеризующихся равенством показателя цвета, можно построить график, отложив по оси абсцисс вычисленные по кривой лучевых скоростей значения DD, а по оси ординат - полученные из фотометрии значения DV. Из (2.4) видно, что точки на графике должны расположиться вдоль прямой, проходящей через начало координат. Угловой коэффициент этой прямой равен -2.17p/R, где R имеет смысл среднего радиуса звезды (в километрах!). У метода Бааде-Весселинка есть несколько "подводных камней". Прежде всего это относится к нашему предположению, что из (B-V)(f1)=(B-V)(f2) следует, что T1=T2 и что различия в блеске связаны только с различиями в размере. (В других модификациях метода вместо подбора пар фаз с одинаковым показателем цвета оценивают, также по показателю цвета, различие в излучающей способности единицы площади поверхности звезды, связанное с различием температуры.) Это предположение требует одинакового закона излучения на двух фазах. Последнее допущение, однако, может быть неверным, что особенно хорошо видно как раз на примере рассмотренной модификации метода Бааде-Весселинка. Одна из двух фаз обязательно приходится на восходящую ветвь кривой блеска, а другая - на нисходящую. На восходящей ветви заметную роль могут играть ударно-волновые процессы, проявляющиеся, в частности, в упоминавшемся появлении эмиссионных линий в спектре. Предложено несколько способов обхода этого "подводного камня". Например, при одинаковом показателе цвета B-V на двух фазах могут отличаться показатели цвета U-B; именно в ультрафиолетовом диапазоне следует ожидать особенно заметного проявления ударно-волновых процессов. Существует "рецепт" выведения из различий ультрафиолетового показателя цвета поправок к кривой блеска. В последние годы в ГАИШ и ИНАСАН наиболее широко используется метод Бааде-Весселинка в модификации, предложенной Л.Балона и доработанной А.С.Расторгуевым; в этом варианте метода существует возможность полностью исключить восходящую ветвь кривой блеска из рассмотрения. Второй "подводный камень" связан с неопределенностью понятия поверхности звезды, в неявном виде постоянно используемого в методе Бааде-Весселинка. Блеск звезды формируется на уровне фотосферы, а линейчатый спектр, на основе которого измеряют лучевые скорости - в более высоких слоях атмосферы. Разные спектральные линии формируются в разных слоях, а плотность атмосферы меняется в течение цикла пульсаций. Влияние этих эффектов на результаты, получаемые при помощи метода Бааде-Весселинка, количественно практически не исследовано. На основе базы данных по фотометрии цефеид, созданной Л.Н.Бердниковым, и самого богатого в мире массива точных измерений лучевых скоростей цефеид, полученного наблюдателями ИНАСАН и ГАИШ с прибором ИЛС, М.Е.Сачков и др. в 1998г. определили, в однородной системе, радиусы 62 цефеид и вывели зависимость период-радиус вида lg R = 1.23 (±0.03) + 0.62 (±0.03) lg P Здесь период выражен в сутках, а радиус - в значениях радиуса Солнца.Выше уже отмечалось, что исследование изменений периода переменной звезды при помощи диаграммы O-C в принципе позволяет надеяться выявить переменность периода, связанную со звездной эволюцией. Для классических цефеид практически исчерпывающие, на ближайшие 20 лет, пока не будет накоплен новый наблюдательный материал, исследования изменяемости периодов выполнены в 1990-х гг. Л.Н.Бердниковым, В.В. Игнатовой и др. Для многочисленных звезд выявлены явные эволюционные изменения периодов, особенно заметные у быстро эволюционирующих звезд - у цефеид с самыми большими периодами. Эволюционные изменения, однако, маскируются переменностью периодов, непосредственно с эволюцией не связанными. Так, практически всегда на эволюционные изменения наложены квазипериодические изменения периодов, с характерными циклами от 10 до 30 лет. Сопоставление наблюдаемой скорости эволюционных изменений периода с теоретическими предсказаниями позволяет отождествить то пересечение полосы нестабильности, на котором находится цефеида. В зависимости от массы звезда может пересекать полосу нестабильности от одного до пяти раз. На нечетных пересечениях полосы нестабильности периоды цефеид должны возрастать, на четных - убывать. В литературе встречаются утверждения, что малоамплитудные цефеиды типа DCEPS - это звезды первого, самого быстрого, пересечения полосы нестабильности, в силу чего они должны показывать быстрые эволюционные изменения периода в сторону увеличения. Оказалось, что это не так. По-видимому, большинство цефеид, увеличивающих периоды, причем как обычных классических цефеид, так и звезд типа DCEPS, находятся на третьем пересечении полосы нестабильности; звезды типа DCEPS пульсируют в первом обертоне, а остальные цефеиды - в основном тоне радиальных пульсаций. Большинство цефеид, уменьшающих период, пересекают полосу нестабильности во второй раз. Согласие между теорией и наблюдениями в отношении скорости изменения периодов вполне удовлетворительно. Что касается причин неэволюционных колебаний периодов, они до конца не ясны. Эффектами на кривой O-C, связанными с орбитальным движением в двойных системах, они не объясняются. В заключение раздела, посвященного классическим цефеидам, расскажем о нескольких необычных звездах. Переменная RS Кормы - классическая цефеида с периодом 41d.38. В 1961г. около нее была обнаружена отражательная туманность, которую в 1972г. детально исследовал Р.Хафлен. Туманность имеет кольцевую структуру, причем яркость колец переменна. По-видимому, туманность состоит из сферических слоев пыли вокруг звезды. Сдвиг фазы изменений яркости деталей колец относительно изменений блеска цефеиды позволяет определить расстояние до RS Кормы чисто геометрическим способом. Найденное Хафленом расстояние согласуется с полученным для ассоциации, в которую входит переменная. Это очень существенно, потому что долгопериодические объекты вроде RS Кормы важны для калибровки зависимости период-светимость. Полярная звезда (a Малой Медведицы) давно была известна как цефеида с малой амплитудой. Согласно 4-му изданию ОКПЗ, ее период равен 3d.97, а амплитуда в лучах V составляет 0m.27. Параметр M-m ее кривой блеска оценивался как 0.50. Это была достаточно типичная звезда типа DCEPS, считавшаяся самой близкой к нам цефеидой. В конце 1980-х гг. было замечено систематическое уменьшение амплитуды Полярной. На основе экстраполяции ожидалось, что к середине 1990-х гг. Полярная практически перестанет быть цефеидой. Высказывались соображения, что Полярная - первый обнаруженный случай прекращения пульсаций цефеиды из-за ее выхода из полосы нестабильности вследствие эволюции. Впрочем, данные последних лет показывают, что уменьшение амплитуды пульсаций Полярной резко остановилось около 1993г., и с тех пор амплитуда изменений ее блеска в лучах V составляет 0m.032, а амплитуда изменений лучевой скорости - около 1.5 км/с. Еще один подобный случай связан со звездой, видимо, все же классической цефеидой (а возможно, и вообще цефеидой) не являющейся. Звезда RU Жирафа примерно до 1965г. не привлекала к себе особенно пристального внимания. Считалось, что это более или менее обычная цефеида с амплитудой около 1m и периодом 22d. Ее положение в Галактике, некоторые фотометрические и спектральные особенности заставляли, правда, предположить, что она может являться цефеидой сферической составляющей. Одна из спектральных особенностей и вовсе необычна для цефеид: в спектре RU Жирафа наблюдались молекулярные полосы углерода. Известно, что в интервале с 1950 по 1962 год амплитуда изменения блеска RU Cam в желтых лучах постепенно нарастала с 1m до 1m.6. В 1963-1964 гг. амплитуда, однако, составляла всего около 0m.55. А в начале 1966г. Ж.Ферни и С.Демер (Канада) сообщили, что RU Cam стала почти постоянной звездой, перестала пульсировать! Последующий анализ показал, что в 1966г. пульсации исчезли не вполне, их амплитуда оставалась близкой к 0m.1, а период оставался прежним, 22d. Очень интересным было поведение RU Cam в следующее десятилетие: у нее чередовались "спокойные" интервалы, в течение которых она меняла блеск с малой амплитудой неправильным образом, и активные интервалы, когда изменения блеска носили квазипериодический характер с амплитудой 0m.2-0m.3 и приблизительно прежним периодом. Предположения, что со временем активные интервалы прекратятся, однако, не оправдались. Звезда остается переменной с амплитудой до 0m.35, временами прослеживаются квазипериоды от 19d.4 до 23d.5 (В данных фотометрии спутника Hipparcos у RU Cam выявлен период 22d.24), но в целом переменность нерегулярна, даже в квазипериодических изменениях бывают сбои фазы до 0.5 цикла. Вероятно, звезду следует отнести к полуправильным переменным, но ее сходство с цефеидами до событий 1960-х годов было необыкновенно большим. Последняя звезда, которую мы рассмотрим в этом разделе, вероятно, имеет с цефеидами еще меньше общего. Это V725 Стрельца, которую открыла на Гарвардской обсерватории Г.Суоп в 1936г. По старому фотографическому материалу удалось проследить ее поведение с 1890г. До 1900г. блеск звезды был примерно постоянен. По немногочисленным оценкам 1900-1926гг. звезда менялась, по-видимому, неправильным образом с амплитудой около 1m. В 1926г. звезда была похожа на цефеиду, ее блеск менялся периодически (P=12d). Самым интересным оказался интервал с 1928 по 1935г. Каждый следующий годовой сезон период оказывался примерно на сутки длиннее, чем в предыдущий раз; в 1935г. период достиг значения в 21d. Амплитуда достигла 2m, причем в основном за счет снижения уровня минимума, так что средняя величина ослабла на ~1m. В 1968-1969гг. V725 Sgr наблюдал все тот же С.Демер. В эти годы средняя величина была поярче, чем в 1935г., но послабее, чем, скажем, в 1900г. Амплитуда изменения блеска была невелика (~0m.4V). Не исключено, что эти наблюдения представляются периодом ~45d-50d. Если это так, то может оказаться, что период продолжал непрерывно нарастать с 1930-х гг. В 1973г. С.Демер и Б.Мадор нашли у звезды P=50d при амплитуде 0m.3V. Сравнительно недавно определенный спектральный класс звезды (G5I-III) не противоречит ее принадлежности ни к цефеидам, ни к рассматриваемым в следующих лекциях полуправильным переменным и звездам типа RV Тельца. |
| Вернуться к оглавлению |
| Перейти к следующей главе |