| Вернуться к оглавлению |
| Перейти к следующей главе |
|
|
Поставим вопрос о влиянии окружающих частиц на число реализующихся уровней и наблюдаемых линий иона или атома, акцентируя внимание на особенностях кулоновского взаимодействия. Такое влияние проявляется в снижении потенциала ионизации и в сдвиге границы серии. Как мы убедились выше, в кулоновском поле ядра электрон имеет бесконечное число дискретных уровней вблизи границы ионизации. Такая структура уровней характерна для любого иона или атома. Действительно, из раздела 13.8 следует, что кулоновский потенциал является хорошим приближением для электростатического поля на больших расстояниях от атомного остатка. Но бесконечное сгущение уровней имеет место лишь в модели уединённой частицы. В действительности электрические поля, создаваемые окружающими частицами, не позволяют реализоваться квантовым состояниям, начиная с некоторой степени возбуждения. Кроме того, как отмечено в разделе 14.1, конечная ширина спектральных линий приводит к их слиянию вблизи границы серии. На рис.14.1.4 видно, как линии, постепенно сближаясь, в конце концов, сливаются, и дискретный спектр переходит в континуум ещё до границы ионизации. Рассмотрим конкретные механизмы «обрезания» спектральных
серий и одновременно уточним представление о характере взаимодействия
заряженных частиц. 17.2 Критерий Инглиса–Теллера
Оценим число наблюдаемых линий, полагая, что их перекрытие
происходит вследствие воздействия микроскопических полей окружающих ионов.
Изменение энергии уровней под влиянием электрического поля называется эффектом
Штарка. Расчёты этого явления методами квантовой механики весьма сложны и будут
описаны в последующих главах. Сейчас мы проведём простые оценки, которые
позволяют выяснить суть дела. Будем считать, что атом водорода окружён однозарядными
ионами. Порядок величины электрического поля можно получить из формулы
где <r> в данном случае — среднее расстояние между ионами. Оно
определяется концентрацией частиц N:
Напряжённость поля можно выразить
как функцию N : Число однозарядных ионов вследствие
электронейтральности плазмы равно числу электронов. Поэтому в данном случае
справедливо Атом водорода на энергетическом уровне с главным квантовым числом n будем рассматривать как электрический диполь, момент d которого равен В поле с напряжённостью E атом приобретает потенциальную энергию Индекс «St» напоминает об эффекте
Штарка. Спектральные линии перекрываются, если потенциальная энергия U достигает размеров энергетической щели
ΔEn,n+1
между двумя соседними уровнями. В случае больших значений n асимптотическая формула для ΔEn,n+1 получается аналогично формуле (14.1.7)
для Δλ: Из условия вытекает окончательная оценка для
главного nSt, начиная с которого уровни
энергии перекрываются: 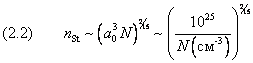 . .
Также перекрываются и линии с верхним уровнем n>nS. Формулу (2.2) называют
критерием Инглиса–Теллера. Она определяет сдвиг границ спектральных серий. 17.3 Плазменная частота
Выше, оценивая влияние на атом окружающих частиц, мы неявно предполагали, что их можно описывать в рамках модели идеального газа. Хотя это предположение в большинстве случаев оказывается верным, но заранее оно совсем не очевидно. Действительно, кулоновский потенциал очень медленно уменьшается с расстоянием, и естественно ожидать, что много заряженных частиц непрерывно влияют друг на друга. Но в модели идеального газа частицы должны взаимодействовать только попарно, причём в течение короткого промежутка времени, пока происходит столкновение. Это, на первый взгляд, серьёзное противоречие решается при более внимательном анализе поведения плазмы. Оказывается, что газ, состоящий из заряженных частиц, в целом электронейтрален. Кроме того, в нём возникают флуктуации заряда, в результате которых частицы противоположных зарядов экранируют друг друга, поэтому силы электростатического взаимодействия быстро падают с расстоянием. Время установления электронейтральности определяется ленгмюровской частотой ω0, а пространственный масштаб — дебаевским радиусом lD. В первой главе мы написали формулу (1.1.2) для плазменной, или ленгмюровской частоты из соображений размерности. Теперь выполним расчёты в рамках модели плоского конденсатора. Хотя эта модель далека от реальных условий, она позволяет наиболее простым способом вычислить величину ω0. Пусть в пространстве между двумя плоскостями находится электронейтральная
плазма. Как и выше, предположим, что плазма состоит из электронов и
однозарядных ионов, поэтому справедлива формула (2.1). Хотя электрическое поле
с одинаковой силой действует на ионы и электроны, но лёгкие электроны
значительно более подвижны. Поэтому в первом приближении мы будем принимать во
внимание только движение электронов. Предположим, что в некоторый момент все электроны,
находящиеся в узком слое толщиной x, сместились относительно
положительных зарядов и расположились на границе слоя, как это показано на рис.17.4.1. 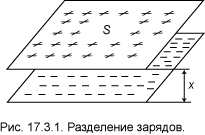
Между плоскостями образуется плоский конденсатор с поверхностной плотностью заряда внутри которого возбуждено электрическое поле На электроны со стороны поля действует возвращающая сила По второму закону Ньютона она вызывает ускорение Мы получили типичное уравнение колебаний, решением которого является гармоническая функция. Её частоту мы уже написали в формуле (1.1.2) первой главы при анализе размерностей. Приведём её ещё раз здесь: 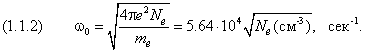
Величина 17.4. Дебаевский радиус
Плазменная частота ω0 является динамической характеристикой плазмы. Существует также статическая характеристика lD, имеющая размерность длины. Она называется дебаевским радиусом, или дебаевской длиной экранирования и определяет масштаб, начиная с которого плазма становится электрически нейтральной. Электронейтральность плазмы как системы зарядов имеет следующий смысл. Внутри объёма, занимаемого плазмой, каждый ион или электрон окружён «шубой» из противоположно заряженных частиц. Суммарный заряд шубы в точности равен заряду частицы (с противоположным знаком), а её размер (по порядку величины) — дебаевскому радиусу. Таким образом, система «заряд–шуба» электронейтральна на расстояниях, превышающих длину экранирования. Оценим величину lD в рассмотренной выше модели плоского конденсатора. При разделении зарядов между обкладками конденсатора возникает потенциальный барьер Частица может его преодолеть, если её
тепловая энергия, пропорциональная температуре T, сравнима
с величиной барьера: Отсюда следует оценка расстояния между обкладками: 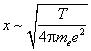 . .
Точные расчёты подтверждают эту оценку, а именно, дебаевский радиус оказывается равным 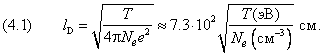
Мы случайно получили точную формулу, хотя все рассуждения имеют силу только как оценки по порядку величины. Смысл параметра lD заключается в следующем. При усреднении по достаточно большим расстояниям плотность числа носителей заряда N можно считать постоянной величиной, но на малых масштабах возможны флуктуации заряда. Сказанное иллюстрируется рис.17.4.1: 
Одинаковое число знаков «+»и «–» во всех строках и столбцах матрицы имитирует квазинейтральность плазмы на масштабах порядка стороны квадрата. Но на небольших расстояниях знаки распределены неравномерно, что указывает на флуктуации заряда. Каждый заряд внутри квадрата окружён «шубой», в которой число противоположных знаков на единицу больше. Дебаевский радиус называют также «длиной экранирования». Смысл этого термина поможет уяснить решение следующей задачи. На левой границе x=0 полупространства, занятого однородной плазмой, находится электрод, создающий в этой плоскости положительный потенциал φ0. (4.2) φ(0) = φ 0. Под влиянием его электрического поля в области x>0 происходит поляризация плазмы, схематически изображённая на рис.17.4.2. 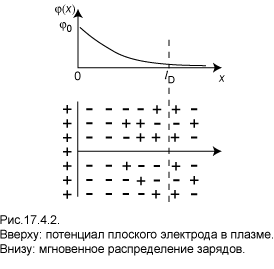
Вблизи границы скапливается избыточное количество электронов, экранирующих поле электрода, но на достаточно больших расстояниях восстанавливается однородная плотность зарядов. На нижней части рисунка приведена как бы мгновенная фотография, отражающая хаотическое расположение частиц на плоскости. Мы рассматриваем только усреднённое по времени распределение зарядов, которое зависит только от одной координаты. Определим масштаб длины экранирования, предполагая плоское одномерное распределение зарядов. Для этого запишем уравнение Пуассона для потенциала φ: создаваемого электронами и однозарядными
ионами По предположению, они находятся в тепловом равновесии. Следовательно, их распределение по координате описывается формулой Больцмана: 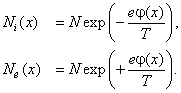
Посредством Ni,e(x) мы обозначили плотность числа ионов и электронов как функцию координаты, а N, как и выше — некоторое «фоновое», усреднённое значение. Подставляя выражения для Ni(x) и Ne(x) в уравнение Пуассона, получим Однако в таком нелинейном виде пользоваться уравнением нельзя. Вспомним, что распределение Больцмана даёт усреднённое по времени значение концентрации. Если φ — соответствующее среднее значение потенциала, то в правой части (4.3) средние значения функций Ni(x) и Ne(x) оказывается заменённым функцией среднего значения. Такая операция допустима исключительно для линейных функций, следовательно, уравнение (4.3) приобретает смысл только после линеаризации. Другими словами, оно справедливо только в случае малого по модулю отношения eφ/T. Раскладывая экспоненты в ряд с точностью до линейных слагаемых, приходим к уравнению в котором введено обозначение В случае плоской симметрии уравнение (4.4) имеет вид Его решением является линейная комбинация Из требования конечности потенциала определяем
константу С2: а из граничного условия (4.2) — константу С1: Окончательно получаем: 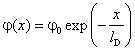 . .
В рассматриваемой модели длина экранирования равна Она в Перейдём к наиболее полной модели, в которой учитывается трёхмерное распределение заряда, а также присутствие произвольного числа компонент плазмы. Произвольно выберем некоторую частицу, заряд которой обозначим q, а её положение примем в качестве центра сферической системы координат. Условие электронейтральности плазмы для «фоновых» значений плотности в общем случае может быть записано в форме где α нумерует компоненты
плазмы. Параметр Zα равен заряду частиц сорта α в
единицах элементарного заряда e. Например,
для электрона После линеаризации с учётом (4.6) снова получаем уравнение (4.4) для самосогласованного поля, но с другим выражением для κ: Решение уравнения (4.4) в случае сферической симметрии выполняется методом, аналогичным тому, который был применён в разделе (16.5). Для функции уравнение самосогласованного поля приводится к виду: Его убывающее на бесконечности
решение равно Константа C теперь определяется из условия, что потенциал вблизи частицы, имеющей заряд q, должен стремиться к кулоновскому: Для электрона а для иона Итак, приходим к окончательному выражению Последняя формула даёт
математическое описание «шубы» размера lD,
состоящей из частиц с противоположным зарядом и схематически изображённой на
рис.17.4.1. На расстояниях меньше дебаевского радиуса поле каждой частицы
определяется кулоновским потенциалом, а при r
> lD оно практически
полностью экранируется «шубой». Теперь мы можем дать более точное определение плазмы как полностью
ионизованного газа, рассматриваемого в масштабах, значительно бόльших
дебаевского радиуса и на временах, более длительных, чем обратная ленгмюровская
частота. 17.5 Снижение потенциала ионизации
Электрон, находящийся в основном состоянии, несомненно, принадлежит
своему атому. Но по мере перехода на всё более возбуждённые состояния он
удаляется от ядра, и на него начинают влиять соседние заряженные частицы.
Электроны, окружающие атом, всё сильнее экранируют поле ядра, и когда радиус
электронной орбиты превышает масштаб экранирования, сила притяжения атомного электрона
к ядру начинает падать с расстоянием по экспоненциальному закону (4.9). Согласно разделу (16.4), бесконечное число уровней вблизи границы ионизации существует только в том случае, если потенциал падает с расстоянием не быстрее, чем 1/r2. В поле (4.9) при r > lD связанные состояния не реализуются, и электрон становится свободным при энергии возбуждения, меньшей потенциала ионизации изолированного атома. Происходит как бы снижение потенциала ионизации. Главное квантовое число последнего возбуждённого состояния можно оценить из условия или В объектах таблицы 17.5.1 штарковское
уширение уровней приводит к большему сдвигу границы серии, чем понижение потенциала
ионизации: nSt<nD. Оценим плотность
газа, при которой оба эффекта дают один и тот же результат. Из условия следует уравнение 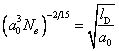 . .
Его решением является плотность числа частиц 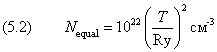 . .
Столь большая величина Nequal реализуется
только для весьма ограниченного круга объектов. Численные оценки
Выполним численные оценки описанных выше параметров плазмы для нескольких конкретных объектов: установки лазерного термоядерного синтеза (ЛТС), управляемого термоядерного синтеза (УТС) с магнитным удержанием плазмы, солнечной короны (СК) и солнечного ветра (СВ). Таблица 17.5.1.
В последней строке таблицы приведены
пространственные масштабы систем, а τ — характерное время длительности процессов.
Хорошо видно, что во всех случаях плазменная частота настолько велика, что
флуктуации заряда за промежуток времени τ многократно сменяют знак и, тем
самым, приводят к «фоновому» значению плотности заряда. Сравнение двух
последних строк показывает, что в перечисленных объектах представление об
электронейтральной плазме соответствует действительности. 17.6 Ионизационное равновесие
В условиях термодинамического равновесия степень ионизации
газа однозначно определяется его температурой и плотностью. Построение теории,
необходимой для вывода уравнений ионизации и диссоциации, было проведено
химиком ван’т Хоффом. В 1919 году Эггертом эти идеи были применены к веществу
звёздных недр, а в 1920 году Сахá установил, что формула для равновесной
ионизации даёт ключ к пониманию спектральной последовательности звёзд. Исключительная
важность этой работы Сахá для астрономии привела к тому, что уравнение
носит его имя. Последовательный вывод формулы Сахá проводится методами
химической термодинамики и выходит за рамки настоящего курса. Здесь мы покажем,
как её можно получить путём не вполне строгих, но физически обоснованных
рассуждений. Равновесные населённости невырожденных уровней Nn и N0 описываются формулой Больцмана: Рассмотрим электрон, который переходит из сильно возбужденного уровня в континуум, где он обладает энергией E. Распространим формулу Больцмана на непрерывный спектр: 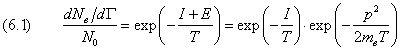
В левую часть входит элемент объема в фазовом пространстве, введённый в формуле (1.2.3) первой главы. Выпишем его ещё раз: Подставив (1.2.3) в (6.1), получим распределение свободных электронов по импульсам: 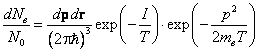 . .
Проинтегрируем это выражение по импульсам и координатам: 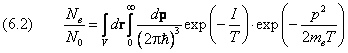 . .
В пространстве импульсов удобно перейти к сферической системе координат. С учётом изотропии интегрирование по угловым переменным сводится к умножению на 4π: Электрон в нашей модели еще не утратил окончательно связи с конкретным атомом. Следовательно, с ним связана область, равная удельному объему иона, который получился из возбуждённого атома: Подставляя (6.3) в (6.2), получим результат интегрирования по пространственным переменным: 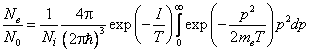 . .
Интеграл в правой части выражается через гамма–функцию. Напомним известную в математике формулу 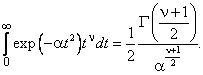
В данном случае ν = 2 и α = (2meT)–1. Следовательно, 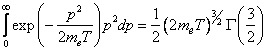 . .
Учитывая, что окончательно получим следующую формулу: 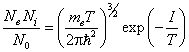 . .
Изначально мы опирались на формулу Больцмана для невырожденных уровней. Для учёта вырождения необходимо каждую из трёх величин: Ne, Ni и N0 — разделить на её статистический вес. Это выполняется с помощью следующих замен: Здесь gi и g0, — статистические веса иона и атома в основном состоянии, а статистический вес электрона полагаем равным двум — числу ориентаций его спина. Произведя замены, получим формулу Сахá: 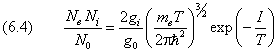 . .
Перепишем её, выразив множитель в скобках через длину волны де Бройля (1.2.8): 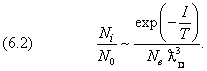
Здесь DD=λD/(π1/2).
Произведение 1)
2)
Присутствие параметра 17.7 Сумма по состояниямПриведём без вывода точное выражение для формулы Сахá, полученное методами химической термодинамики: 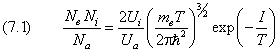 . .
В знаменателе левой части стоит Na
— полная плотность числа атомов,
просуммированная по всем его возможным состояниям. Величина Ni теперь равна сумме числа ионов во всех состояниях. В правой части
статистические веса иона и атома в определённом (основном) состоянии заменены статистическими суммами: Здесь индекс k нумерует все энергетические уровни иона или атома. Расходимость суммы по состояниямКак мы уже знаем, уровни возбуждённых состояний сходятся к пределу ионизации. Примем за точку отсчёта энергию основного состояния. С такой точкой отсчёта энергия k–го уровня атома водорода равна Если температура низка в сравнении с потенциалом ионизации, то слагаемые суммы (7.2) быстро уменьшаются по величине и после немногих первых членов становятся пренебрежимо малыми. Может возникнуть впечатление, что сумма по состояниям сходится. Но это не так, в чём легко убедиться, заменив в (7.2) все энергии уровней на потенциал ионизации. Сумма ряда, если она существует, от такой операции может только уменьшиться. Следовательно, справедливо неравенство из которого вытекает расходимость суммы по состояниям. Этот результат справедлив для всех ионов и атомов, так как их возбуждённые состояния вблизи границы ионизации хорошо описываются в модели атома водорода. Причина расходимости ряда (7.2) ясна из предыдущего материала. Бесконечное множество уровней существует только в уединённом атоме, следовательно, сумма (7.2) содержит только конечное число слагаемых. По существу рассматриваемый вопрос выходит за рамки
формальной термодинамики, и его решение требует строгого определения того,
какой электрон считать свободным и какой — связанным. Это определение в свою очередь
зависит от конкретной постановки задачи, для которой рассчитывается
ионизационное равновесие. Так, в задаче о проводимости плазмы свободными надо
считать электроны, способные проводить электрический ток. В задаче об излучении плазмы связанными следует считать электроны, испускающие дискретные линии, а свободными — электроны, дающие непрерывный спектр. Если электрон находится на одном из верхних возбуждённых уровней, то у него есть определенная вероятность либо «свалиться» на какой-нибудь из нижних уровней с испусканием кванта дискретного спектра, либо подвергнуться ионизации, в результате которой он окажется свободным и сможет испустить квант непрерывного спектра. Наиболее последовательным представляется решение вопроса методами физической кинетики. Находятся вероятности переходов между дискретными уровнями, вероятность излучения с переходом на все нижележащие уровни и вероятность ионизации с учетом всех возможных процессов. К ним относятся удары электронов и быстрых ионов, а также ионизация тепловым и резонансным излучением, воздействие флуктуирующих микрополей. С учетом всех перечисленных процессов вычисляются заселенности высших возбужденных уровней. В расчет входят величины, характеризующие уже не равновесие, а вероятности различных процессов. В последующих главах мы рассмотрим эти процессы, а также покажем сравнительно простой способ вычисления всех необходимых вероятностей. Наибольшей вероятностью обладают переходы между соседними уровнями (при которых как главное, так и азимутальное квантовые числа меняются на единицу). Поэтому основное значение имеет процесс, который можно назвать диффузией электрона по верхним возбужденным уровням. Ионизация быстро движущихся атомов может происходить и под действием постоянного магнитного поля. В сопутствующей системе координат на атом действует электрическое поле. Если это поле создает на длине, равной радиусу электронной орбиты, разность потенциалов, достаточную для ионизации, то постоянное магнитное поле может оторвать электрон с высокого возбужденного уровня (лоренцева ионизация). Итак, для расчётов состояния газа требуется знать структуру
ионов и атомов, а также характер их взаимодействия друг с другом и с полем
излучения. |
| Вернуться к оглавлению |
| Перейти к следующей главе |