| ||
|
|
|
К.В.БЫЧКОВ
[ГАИШ],
А.С.НИФАНОВ,
И.М.САРАЕВА [физфак МГУ]
|
|
Предлагается
несколько задач для семинарских занятий со студентами – астрономами по теме
«Динамика материальной точки». В основе
статьи – накопленный авторами опыт семинарских занятий по курсу общей физики и
астрономии со студентами астрономического отделения физического факультета МГУ.
В задачах рассматривается движение
материальной точки в гравитационном (и кулоновском) поле. Эти задачи являются
важными элементами фундамента для изучения курса современной астрономии. В
задачах обсуждаются события, реально наблюдаемые астрономами. Так задача о прецессии орбиты имеет
прямое отношение к объяснению траектории движения вокруг Солнца его ближайшей
планеты – Меркурия. В задаче о гравитационном взаимодействии движущихся масс
рассматривается ситуация, часто реализующаяся в космическом пространстве. В некоторых
случаях два взаимодействующих тела можно
рассматривать, пренебрегая в первом приближении влиянием других тел. Так,
например, у двойных звезд траектории в основном определяется их гравитационным взаимодействием. Кроме того, движение каждой планеты Солнечной системы
происходит, в первую очередь, под влиянием ее притяжения к Солнцу, другие тела
вызывают лишь малые искажения эллиптичности орбиты. При решении задач используется, как
уже известный, материал семинара «Кинематика материальной точки»,
опубликованный ранее [3]. Задача 1.
Планета массы
Рис. 2. Движение по эллиптической орбите, вращающейся
вокруг центра сил O относительно
неподвижной системы координат. |
|
движется под действием
гравитационного притяжения планетой массы 
(рис.4), то 
- интеграл движения, где 
- скорость планеты массы , 
- расстояние между
планетами. Примечание: интеграл движения – это некоторая функция координат и
скоростей, сохраняющая свою величину постоянной. Например, в соответствии со
вторым законом Кеплера, в поле центральных сил интегралом движения является 
, 
- абсолютная угловая скорость.
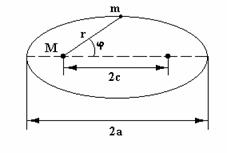
Рис.4. Движение массы
в гравитационном поле планеты массы .
Умножим обе части этого уравнения
скалярно на 
,
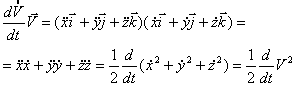точка над
координатой обозначает дифференцирование по времени. Аналогичным образом
получаем:
или иначе это можно
записать как 
Итак, получим, 
или 
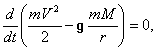т.е.
- интеграл движения.
Если 
то 
При 
должно быть 
что невозможно.
Итак, при 
тело может двигаться лишь в ограниченной области
пространства, такое движение называется финитным.
Если 
возможно, такое
движение называется инфинитным.
, совершающего движение в поле гравитационного притяжения
массой , если задана величина интегралов движения 
и 
(см. предыдущую
задачу).
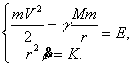
или 
В перигелии и
афелии 
и, следовательно, 
Зависимость 
от при 
представлена на рис.
5.
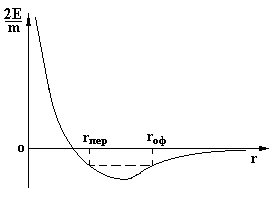
Рис. 5 График зависимости
от при 
Проанализируем полученное квадратное уравнение:
где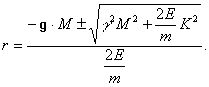 
При
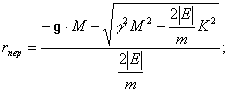
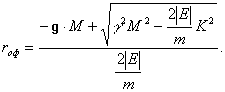
При 
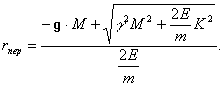
При 
Задача 4. Доказать, что
эксцентриситет 
траектории, по которой
движется планета массы , в гравитационном поле планеты массы 
связан с интегралами
движения и следующим образом 
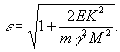
При движении по
эллипсу () эксцентриситет 
(см. рис. 4) и,
следовательно,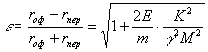 
(см. задачу 3).
При движении по
гиперболе () в перигелии:
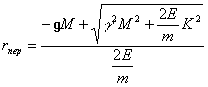, кроме того
где 
(см. [3], задача 6)
После несложных
преобразований получаем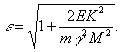
Задача 5 Тело массы движется по гиперболе в гравитационном поле
массы (рис.6). Известна скорость тела 
на бесконечном
удалении от притягивающего центра (тела массы ), а также прицельное расстояние 
. Определить угол рассеяния 
. Примечание: прицельным расстоянием называется кратчайшее
расстояние от притягивающего центра до касательной к траектории в бесконечно удаленной
точке.
Рис.6 Движение тела массы
по
гиперболе в гравитационном поле
тела массы 
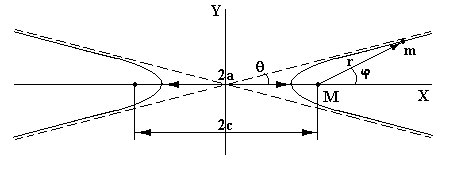
На бесконечном
удалении от притягивающего центра угол 
имеет минимальное значение
и равен 
. С другой стороны, при 
, что следует из
уравнения гиперболической траектории. Таким образом, задача определения 
сводится к определению
эксцентриситета гиперболы 
.
Из решения
задачи 4 следует, что
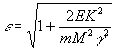(3)
Поскольку
движение происходит в поле центральной силы, момент импульса 
массы относительно
притягивающего центра сохраняется. По определению, величина 
.
На бесконечном расстоянии от притягивающего центра
; 
; 
.
С учетом этих равенств из (3) получаем:
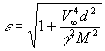, отсюда 
,
Задача 6 Два тела с массами 
и 
взаимодействуют по
закону гравитации. При этом оба тела совершают в пространстве финитное
движение. Найти траектории тел.
Поместим начало
координат в центр масс системы. Через 
и
обозначим радиус-векторы тел 
и 
соответственно. Тогда,
по определению центра масс, 
, откуда 
. Введем в рассмотрение вектор 
длины 
направленный от массы к массе (рис. 7). После
несложных преобразований получим 
Уравнения движения
каждого из тел можно записать следующим образом:
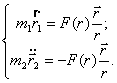, где 
(4).
Из системы (4) следует уравнение
(5) .
Поместим начало
вектора 
в центр масс системы. В соответствии с уравнением движения
(5) описывает эллипс вокруг центра масс как фокуса. Уравнение эллипса в
полярных координатах имеет вид 
.
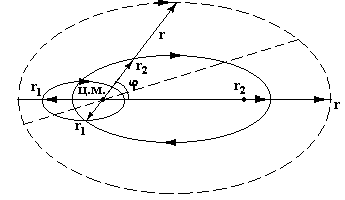
Рис.7
Траектории материальных точек с массами
и , взаимодействующих по закону гравитации.
По разные
стороны от центра масс вдоль 
будем откладывать 
и 
(рис. 7). Поскольку 
и 
, легко понять, что и движутся по эллиптическим
орбитам, один из фокусов которых совпадает с центром масс системы и
Литература:
1.
Сивухин Д.В. Общий курс физики. Том 1. Механика.3-изд.,
М.: Наука, 1989.
2. Киттель Ч., Найт У., Рудерман М. Механика. М.: Наука. 1971.
3. Бычков К.В., Сараева И.М. // Физическое образование в ВУЗах, Т.5, N2, 1999. С. 146-161.
|
|
. Как нужно изменить величину силы, чтобы относительное
движение по орбите осталось неизменным, а орбита, не изменяя своего вида,
вращалась вокруг центра сил 
, уравнения движения планеты по вращающейся эллиптической
орбите примут вид:
.
